数组 | Cheyennee

问题：二分查找

问题描述：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例1：

1
2
3

输入: nums = [-1,0,3,5,9,12], target = 9     
输出: 4       
解释: 9 出现在 nums 中并且下标为 4

示例2：

1
2
3

输入: nums = [-1,0,3,5,9,12], target = 2     
输出: -1        
解释: 2 不存在 nums 中因此返回 -1

提示：

1
2
3

- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。

二分法使用的条件/场景：

1 2	- 数组为有序数组 - 若要返回唯一下标，则数组中应该无重复元素

二分法的重点：

1	- 把握查找区间，根据区间的定义来做边界情况的处理

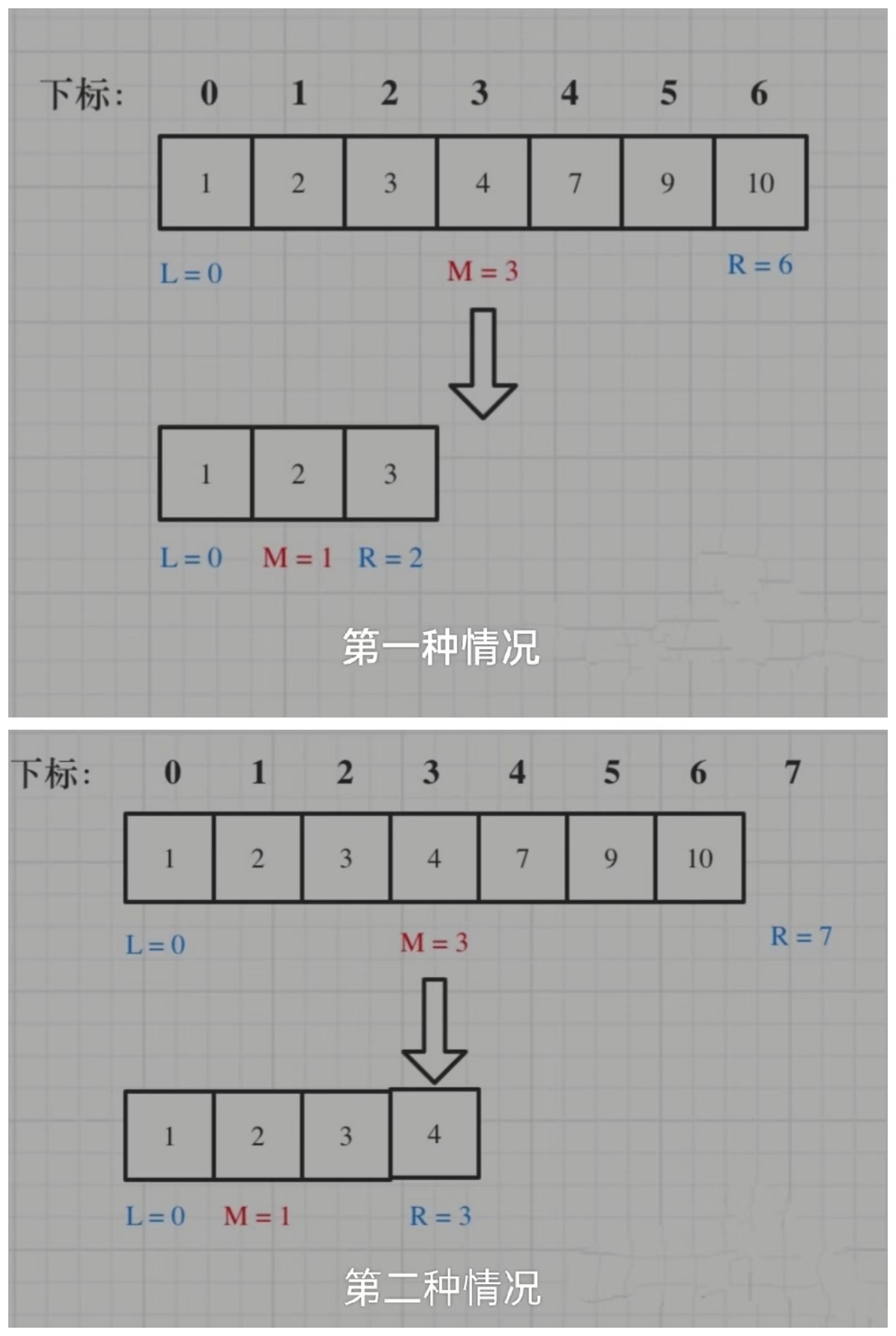
二分法的两种情况

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */

/*
	1. [left, right]
	在这种情况下，while(left<=right)，因为left==right是有意义的
	if(nums[middle]>target)时，right=middle-1，因为当前nums[middle]一定不是target
	初始时，right=nums.length-1
*/
var search = function(nums, target){
    let mid, left=0, right=nums.length-1;
    while (left<=right){
        //此处使用位运算符可以防止大数溢出
        mid = left + ((right-left)>>1)
        if(nums[mid]>target)
            right = mid-1;
        else if(nums[mid]<target)
            left = mid+1;
        else
            return mid;
    }
    return -1;
}

/*
	2. [left, right)
	在这种情况下，while(left<right)，因为left==right是没有意义的
	if(nums[middle]>target)时，right=middle，因为当前nums[middle]不等于target，去左区间继续寻找
	初始时，right=nums.length
*/
var search = function(nums, target){
    let mid, left=0, right=nums.length;
    while(left<right){
        mid=left+((right-left)>>1);
        if (nums[mid]>target)
            right=mid;
        else if(nums[mid]<target)
            left=mid+1;
        else
            return mid;
    }
    return -1;
}

解析：

情况解析图

问题：二分查找II

描述：

请实现有重复数字的升序数组的二分查找。给定一个 元素有序的（升序）长度为n的整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的第一个出现的target，如果目标值存在返回下标，否则返回 -1。

示例：

1
2
3

输入：[1,2,4,4,5],4
返回值：2
说明：从左到右，查找到第1个为4的，下标为2，返回2

解法：

function binary(nums, target){
    if(!nums||nums.length)
        return -1;
    let left = 0;
    let right = nums.length-1;
    while(left<right){
        let mid = left+Math.floor((right-left)/2);
        if(nums[mid]<target)
            left=mid+1;
        else
            right=mid;
    }
    return nums[left]===target?left:-1;
}

问题：移除元素

问题描述：给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。

示例1：

1 2	输入：nums = [3,2,2,3], val = 3 输出：输出数组中不等于val的元素个数为2, 且 nums 中的前两个元素均为 2。

解法：

//快慢指针
var removeElement = (nums, val)=>{
    let k = 0;
    for(let i=0;i<nums.length;i++){
        if(nums[i]!=val){
            nums[k++]=nums[i]
        }
    }
    return k;
}

问题：有序数组的平方

问题描述：给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。

示例：

1
2
3

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100] 
解释：平方后，数组变为 [16,1,0,9,100]，排序后，数组变为 [0,1,9,16,100]

解法一：暴力法：先平方后排序

var sortedSquares = nums=>{
	for(let i=0;i<nums.length;i++)
		nums[i] *= nums[i];
	//sort方法会按照字符串序列来排序，这不是正常人所期望的
    //回调函数a-b是升序排列
	nums.sort((a,b)=>a-b)
	return nums;
}

解法二：双指针法：由于数组是有序的，所以数组平方后的最大值就在数组的两端

var sortedSquares = nums => {
	let n = nums.length;
	let i=0, j=n-1, k=n-1.;
	let res = new Array(n).fill(0);
	while(i<=j){
		let left = nums[i]*nums[i], right = nums[j]*nums[j];
		if(left<right){
			nums[k--] = right;
			j--;
		}else{
			nums[k--] = left;
			i++;
		}
	}
	return res;
}

问题：长度最小的子数组

问题描述：给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例

1
2
3

输入：s = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

解法：滑动窗口

/*
	所谓滑动窗口，就是不断调整子序列的起始位置和终止位置
	滑动窗口需要确定：1)窗口内是什么？2)如何移动窗口的起始位置？3)如何移动窗口的结束位置？
	1)窗口就是满足其和>=s的最小连续子数组2)如果当前窗口的值大于s了，窗口就要向前移动了3)for循环里的索引就是窗口的结束位置
	时间复杂度为o(n)
*/
var minSubArrayLen = function(target, nums){
    let length = nums.length;
    let sum=0, res=length+1, start=0;
    for(let i=0;i<length;i++){
        sum+=nums[i];
        while(sum>=target){
            res = Math.min(res, i-start+1);
            sum-=nums[start++];
        }
    }
    return res>length?0:res;
}

问题：螺旋矩阵

描述：

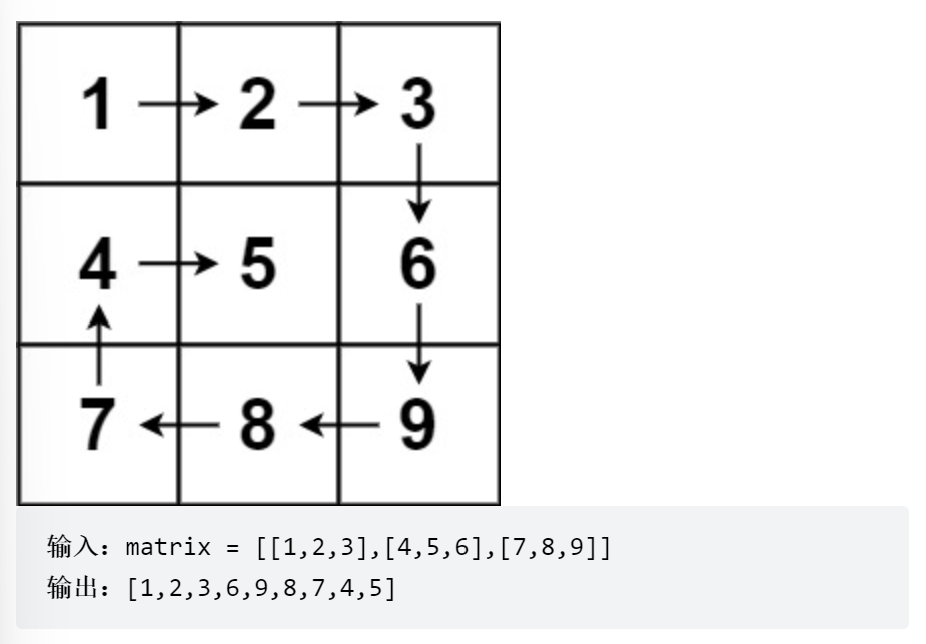
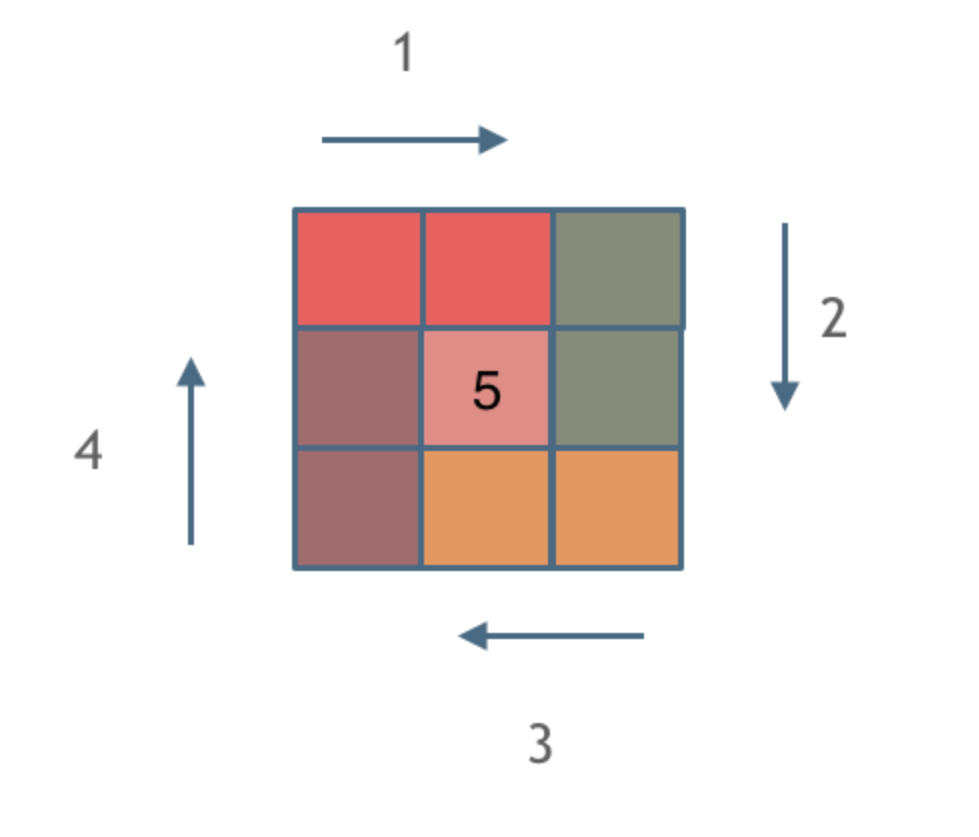
1	给你一个 m 行 n 列的矩阵 matrix ，请按照顺时针螺旋顺序，返回矩阵中的所有元素。

示例：

螺旋矩阵

解法：

var spiralOrder = function(matrix) {
    let m = matrix.length;
    let n = matrix[0].length;
    let offset = 1;
    let res = [];
    let startX = 0, startY = 0;
    let loop = Math.floor(Math.min(m, n)/2);
    let mid = loop;
    let count = 0;
    let i, j;
    while(loop--){
        for(j=startY;j<startY+n-offset;j++)
            res[count++]=matrix[startX][j];
        for(i=startX;i<startX+m-offset;i++)
            res[count++]=matrix[i][j];
        for(;j>startY;j--)
            res[count++]=matrix[i][j];
        for(;i>startX;i--)
            res[count++]=matrix[i][startY];
        startX++;
        startY++;
        offset+=2;
    }
    if(Math.min(m, n)%2){
        if(m>n){
            // 如果行大于列，则给中间列赋值
            for(let i=mid;i<mid+m-n+1;i++)
                res[count++]=matrix[i][mid];
        }else{
            for(let i=mid;i<mid+n-m+1;i++)
                res[count++]=matrix[mid][i];
        }
    }
    return res;
};

问题：螺旋矩阵II(与I的区别在于这里的矩阵的长度和宽度是相等的)

问题描述：给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

示例：

1 2	输入：3 输出：[ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]

思路

1	坚持循环不变量原则，我们要画四条边，每画一条边都要坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来。

循环图示

解法

var generateMatrix = function(n){
    //起始位置
	let startX = startY = 0 ;
    //旋转圈数
    let loop = Math.floor(n/2);
    //中间位置
    let mid = Math.floor(n/2);
    //控制每一层填充元素的个数,每次循环右边界都会收缩一位
    let offset = 1;
    //更新填充数字
    let count = 1;
    let res = new Array(n).fill(0).map(()=>new Array(n).fill(0));
    while(loop--){
        let row = startX, col = startY;
        //上行从左到右（左闭右开）
        for(;col<startY+n-offset;col++)
            res[row][col]=count++;
        //右列从上到下（左闭右开）
        for(;row<startX+n-offset;row++)
            res[row][col]=count++;
        //下行从右到左（左闭右开）
        for(;col>startY;col--)
            res[row][col]=count++;
        //左列从下到上（左闭右开）
        for(;row>startX;row--)
            res[row][col]=count++;
        //更新起始位置
        startX++;
        startY++;
        //更新offset，每个循环之后会往左往右各缩一格
        offset+=2;
    }
    //如果n为奇数的话，需要单独给矩阵最中间的位置赋值
    if(n%2===1)
        res[mid][mid]=count;
    return res;
}

最大数

描述：

1
2

给定一组非负整数 nums，重新排列每个数的顺序（每个数不可拆分）使之组成一个最大的整数。
注意：输出结果可能非常大，所以你需要返回一个字符串而不是整数。

示例：

1 2	输入：nums = [10,2] 输出："210"

解法：

var largestNumber = function(nums){
    nums.sort((a,b)=>{
        let x1 = a+''+b;
        let x2 = b+''+a;
        return x2-x1;
    })
    let res = nums.join("");
    return res.charAt(0)==='0'?'0':res;
}

移动零

描述：

1
2

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。
请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例：

1 2	输入: nums = [0,1,0,3,12] 输出: [1,3,12,0,0]

解法：

var moveZeroes = function(nums) {
    let slow=fast=0;
    while(fast<nums.length){
        if(nums[fast]!==0){
            nums[slow++]=nums[fast];
        }
        fast++;
    }
    for(let i=slow;i<nums.length;i++)
        nums[i]=0;
    return nums;
};

合并两个有序的数组

描述：

给出一个有序的整数数组 A 和有序的整数数组 B ，请将数组 B 合并到数组 A 中，变成一个有序的升序数组

注意：
1.保证 A 数组有足够的空间存放 B 数组的元素， A 和 B 中初始的元素数目分别为 m 和 n，A的数组空间大小为 m+n
2.不要返回合并的数组，将数组 B 的数据合并到 A 里面就好了，且后台会自动将合并后的数组 A 的内容打印出来，所以也不需要自己打印
3. A 数组在[0,m-1]的范围也是有序的

示例：

输入：[4,5,6],[1,2,3]
返回值：[1,2,3,4,5,6]
说明：
A数组为[4,5,6]，B数组为[1,2,3]，后台程序会预先将A扩容为[4,5,6,0,0,0]，B还是为[1,2,3]，m=3，n=3，传入到函数merge里面，然后请同学完成merge函数，将B的数据合并A里面，最后后台程序输出A数组

思路：

从后往前放置元素可以保证顺序

解法：

function merge( A, m, B, n ) {
    // write code here
    let i = m-1;
    let j = n-1;
    let p = m+n-1;
    while(i>=0&&j>=0){
        if(A[i]>B[j]){
            A[p]=A[i];
            p--;
            i--;
        }else{
            A[p]=B[j];
            p--;
            j--;
        }
    }
    // 此处无需判断i>=0的情况，因为A中已包含
    while(j>=0){
        A[p]=B[j];
        p--;
        j--;
    }
}

求平方根[二分查找]

链接：

求平方根

描述：

实现函数 int sqrt(int x)，计算并返回 x 的平方根（向下取整）。

示例：

1 2	输入：2 返回值：1

解法：

function sqrt( x ) {
    if(x===1)
      return 1;
    let left = 1, right = x;
    while(left<=right){
      // 求mid的条件与二叉查找不同
      let mid = Math.floor((right+left)/2);
      if((mid*mid<=x)&&((mid+1)*(mid+1)>x))
        return mid;
      else if((mid*mid)<x)
        left = mid+1;
      else
        right = mid-1;
    }
    return 0;
}

合并两个有序数组

解法：

function merge( A, m, B, n ) {
    // write code here
    let i = m-1;
    let j = n-1;
    let p = m+n-1;
    while(i>=0&&j>=0){
        if(A[i]>B[j]){
            A[p]=A[i];
            p--;
            i--;
        }else{
            A[p]=B[j];
            p--;
            j--;
        }
    }
    while(j>=0){
        A[p]=B[j];
        p--;
        j--;
    }
}

合并区间

描述：

1	给出一组区间，请合并所有重叠的区间。请保证合并后的区间按区间起点升序排列。

示例：

1 2	输入：[[10,30],[20,60],[80,100],[150,180]] 返回值：[[10,60],[80,100],[150,180]]

解法：

function merge(intervals){
    let res = [];
    if(intervals.length===0)
        return res;
    intervals.sort((a,b)=>{
        if(a.start!==b.start)
            return a.start-b.start;
        return a.end - b.end;
    })
    res.push(intervals[0]);
    let count = 0;
    for(let i=1;i<intervals.length;i++){
        let now = intervals[i];
        let old = res[count];
        if(now.start>old.end){
            res.push(now);
            count++;
        }else{
            res.pop();
            let newInter = new Interval(old.start, now.end>old.end?now.end:old.end);
            res.push(newInter);
        }
    }
    return res;
}

在两个长度相等的排序数组中找到上中位数

描述：

1
2

给定两个递增数组arr1和arr2，已知两个数组的长度都为N，求两个数组中所有数的上中位数。
上中位数：假设递增序列长度为n，为第n/2个数。奇数为n/2+1,偶数为n/2。

示例：

1
2
3

输入：[1,2,3,4],[3,4,5,6]
返回值：3
说明：总共有8个数，上中位数是第4小的数，所以返回3。

解法：

function findMedianinTwoSortedAray( arr1 ,  arr2 ) {
    let len1 = arr1.length;
    let len2 = arr2.length;
    let mid_index = (len1+len2)%2?Math.floor((len1+len2)/2)+1:Math.floor((len1+len2)/2);
    let index = 0;
    let res = arr1[0];
    let index1 = 0, index2 = 0;
    while(index1<len1&&index2<len2){
        if(arr1[index1]<arr2[index2]){
            res = arr1[index1];
            index1++;
        }else{
            res = arr2[index2];
            index2++;
        }
        if(index === mid_index-1)
            return res;
        index++;
    }
    if(index1<len1)
        return arr1[index1+mid_index-1-index];
    else
        return arr2[index2+mid_index-1-index];
}