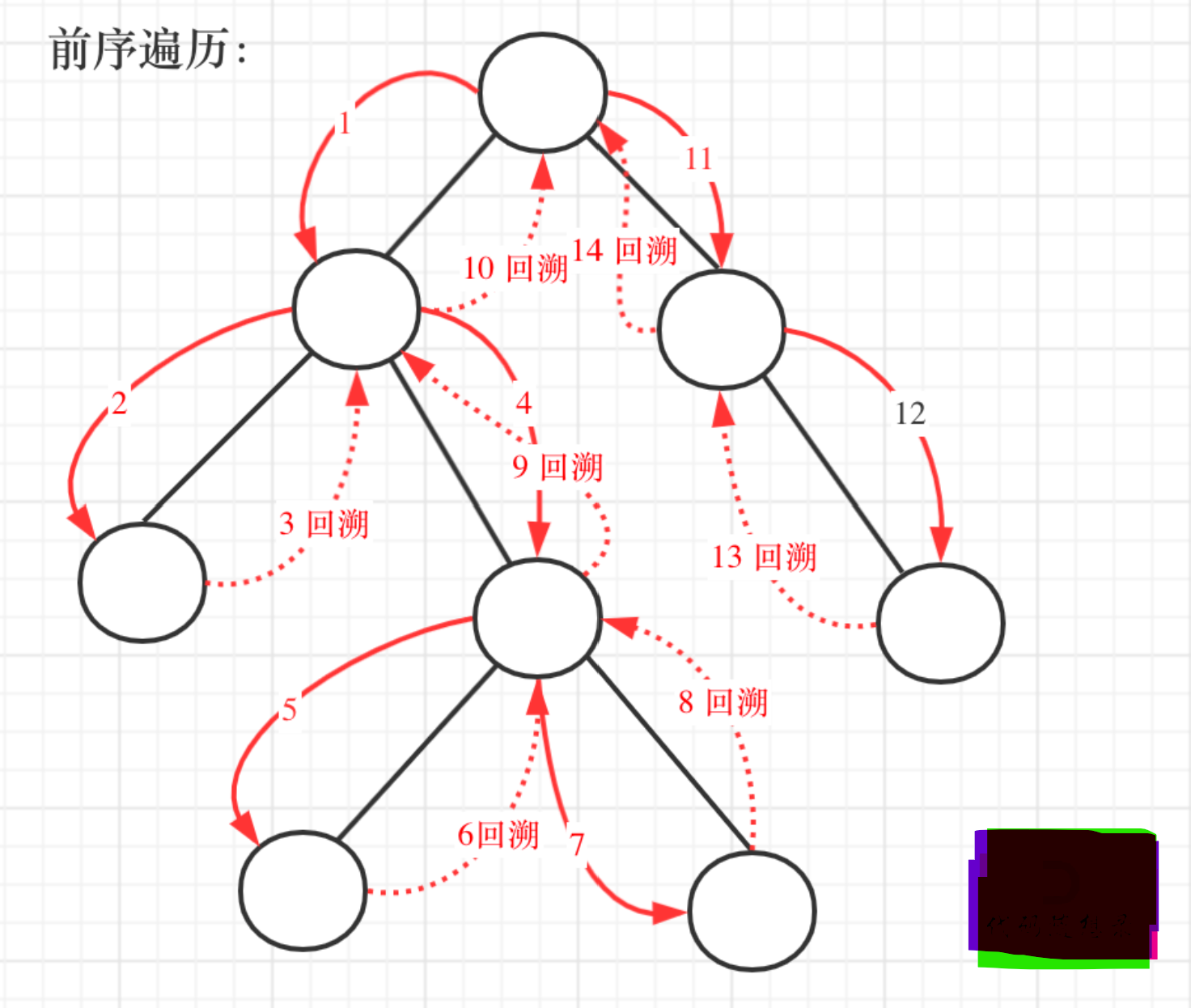
回溯使用先序遍历，二叉搜索树使用中序遍历

二叉树的递归遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
//前序遍历
var preorderTraversal = function(root){
    let res = [];
    const dfs = function(root){
        if(!root)
            return ;
        res.push(root.val);
        dfs(root.left);
        dfs(root.right);
    }
    dfs(root);
    return res;
}

//中序遍历
var inorderTraversal = function(root){
    let res = [];
    const dfs = function(root){
        if(!root)
            return;
        dfs(root.left);
        res.push(root.val);
        dfs(root.right);
    }
    dfs(root);
    return res;
}

//后序遍历
var postorderTraversal = function(root){
    let res = [];
    const dfs = function(root){
        if(!root)
            return;
        dfs(root.left);
        dfs(root.right);
        res.push(root.val);
    }
    dfs(root);
    return res;
}

二叉树的迭代遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
//前序：栈，根，右孩子先进栈
// 入栈 右 -> 左
var preorderTraversal = function(root, res=[]){
    if(!root)
        return res;
    const stack = [root];
    let cur = null;
    while(stack.length){
        cur = stack.pop();
        res.push(cur.val);
        cur.right && stack.push(cur.right);
        cur.left && stack.push(cur.left);
    }
    return res;
}


//中序
// 入栈 左 -> 右
// 出栈 左 -> 中 -> 右
var inorderTraversal = function(root, res=[]){
    const stack = [];
    let cur = root;
    while(stack.length||cur){
        if(cur){
            stack.push(cur);
            cur = cur.left;
        }else{
            cur = stack.pop();
            res.push(cur.val);
            cur = cur.right;
        }
    }
    return res;
}

//后序
/*
    先序遍历是中左右，后续遍历是左右中
    调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，
    然后在反转result数组，输出的结果顺序就是左右中
*/
var postorderTraversal = function(root, res=[]){
    if(!root)
        return res;
    const stack = [root];
    let cur = null;
    do{
        cur = stack.pop();
        res.push(cur.val);
        cur.left && stack.push(cur.left);
        cur.right && stack.push(cur.right);
    }while(stack.length);
    return res.reverse();
}

二叉树统一迭代遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
// 前序遍历：中左右
// 压栈顺序：右左中
var preorderTraversal = function(root, res = []){
    if(!root)
       	return res;
    const stack = [root];
    while(stack.length){
        const node = stack.pop();
        if(!node){
            res.push(stack.pop().val);
            continue;
        }
        node.right && stack.push(node.right);//右
        node.left && stack.push(node.left);//左
        //处理节点(将元素放进结果集)放入栈之后，紧接着放入一个空指针作为标记
        stack.push(node);//中
        stack.push(null);
    }
    return res;
}

var inorderTraversal = function(root, res = []){
    if(!root)
        return res;
    const stack = [root];
    while(stack.length){
        const node = stack.pop();
        if(!node){
            res.push(stack.pop().val);
            continue;
        }
        node.right && stack.push(node.right);
        stack.push(node);
        stack.push(null);
        node.left && stack.push(node.left);
    }
    return res;
}

var postorderTraversal = function(root, res = []){
    if(!root)
        return res;
    const stack = [root];
    while(stack.length){
        const node = stack.pop();
        if(!node){
            res.push(stack.pop().val);
            continue;
        }
        stack.push(node);
        stack.push(null);
        node.right && stack.push(node.right);
        node.left && stack.push(node.left);
    }
    return res;
}

二叉树的层次遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 迭代
var levelOrder = function(root){
    let res = [];
    let queue = [];
    queue.push(root);
    while(queue.length){
        let length = queue.length;
        let curLevel = [];
        for(let i=0;i<length;i++){
            let node = queue.shift();
            curLevel.push(node.val);
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
        res.push(curLevel);
    }
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
var levelOrder = function(root){
    let res = [];
    function helper(root, level, res){
        if(!root)
            return;
        if(res.length<level+1)
            res.push([]);
        res[level].push(root.val);
        helper(root.left, level+1, res);
        helper(root.right, level+1, res);
    }
    helper(root, 0, res);
    return res;
}

翻转二叉树

​ 这道题目使用前序遍历和后序遍历都可以，唯独中序遍历不方便，因为中序遍历会把某些节点的左右孩子翻转了两次！

递归过程：

  1. 确定递归函数的参数和返回值
  2. 确定终止条件
  3. 确定单层递归的逻辑

迭代：

​ 使用层次遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//递归
var invertTree = function(root){
    if(!root)
        return null;
    const rightNode = root.right;
    root.right = invertTree(root.left);
    root.left = invertTree(rightNode);
    return root;
}

//层次遍历
const inverNode = function(root, left, right){
    [left, right] = [right, left];
    root.left = left;
    root.right = right;
}
var invertTree1 = function(root){
    let queue = [];
    if(!root)
        return root;
    queue.push(root);
    while(queue.length){
        let length = queue.length;
        while(length--){
            let node = queue.shift();
            inverNode(node, node.left, node.right);
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return root;
}

对称二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// 递归
var isSymmetric = function(root){
    const compareNode = function(left, right){
        if(left===null&&right!==null||left!==null&&right===null)
            return false;
        else if(left===null&&right===null)
            return true;
        else if(left.val!==right.val)
            return false;
        let outSide = compareNode(left.left, right.right);
        let innerSide = compareNode(left.right, right.left);
        return outSide&&innerSide;
    }
    if(!root)
        return true;
    return compareNode(root.left, root.right);
}

//迭代
var isSymmetric1 = function(root){
    if(!root)
        return true;
    let queue = [];
    queue.push(root.left);
    queue.push(root.right);
    while(queue.length){
        let leftNode = queue.shift();
        let rightNode = queue.shift();
        if(leftNode===null&&rightNode===null)
            continue;
        if(leftNode===null||rightNode===null||leftNode.val!==rightNode.val)
            return false;
        queue.push(leftNode.left);
        queue.push(rightNode.right);
        queue.push(leftNode.right);
        queue.push(rightNode.left);
    }
    return true;
}

二叉树的最大深度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 递归
var maxdepth = function(root){
    if(!root)
        return 0;
    let leftDepth = maxdepth(root.left);
    let rightDepth = maxdepth(root.right);
    return 1 + Math.max(leftDepth, rightDepth);
}

//迭代：层次遍历
var maxDepth = function(root){
    let queue = [root];
    let count = 0;
    while(queue.length){
        let size = queue.length;
        count++;
        while(size--){
            let node = queue.shift();
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return count;
}

二叉树的最小深度

​ 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。说明: 叶子节点是指没有子节点的节点。

示例：

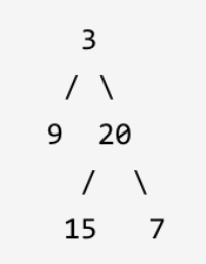
1
给定二叉树 [3,9,20,null,null,15,7]，返回它的最小深度 2。
最小深度 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 递归
var minDepth = function(root){
    if(!root)
        return 0;
    if(!root.left && !root.right)
        return 1;
    if(!root.left)
        return 1+minDepth(root.right);
    if(!root.right)
        return 1+minDepth(root.left);
    return 1+Math.min(minDepth(root.left), minDepth(root.right));
}


// 迭代：层次遍历
var minDepth1 = function(root){
    if(!root)
        return 0;
    const queue = [root];
    let dep = 0;
    while(true){
        let size = queue.length;
        dep++;
        while(size--){
            const node = queue.shift();
            if(!node.left&&!node.right)
                return dep;
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
}

完全二叉树的节点个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// 递归
var countNodes = function(root){
    if(!root)
        return 0;
    let leftNodes = countNodes(root.left);
    let rightNodes = countNodes(root.right);
    return 1+leftNodes+rightNodes;
}

// 迭代：层次遍历
var countNodes1 = function(root){
    if(!root)
        return 0;
    let queue = [root];
    let count = 0;
    while(queue.length){
        let length = queue.length;
        count += length;
        while(length--){
            let node = queue.shift();
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return count;
}

// 递归：利用完全二叉树的性质
/**
 * 判断一棵树是不是完全二叉树，只要判断其左子树左遍历与右子树右遍历的高度是否一致
 * 因为如果完全二叉树是满二叉树的话可以直接使用公式计算
 * 
 */
var countNodes2 = function(root){
    if(!root)
        return 0;
    let left = root.left;
    let right = root.right;
    let leftDepth = 0, rightDepth = 0;
    while(left){
        left = left.left;
        leftDepth++;
    }
    while(right){
        right = right.right;
        rightDepth++;
    }
    if(leftDepth===rightDepth)
        return Math.pow(2, leftDepth+1)-1;
    return 1+countNodes2(root.left)+countNodes2(root.right);
}

求深度适合用前序遍历，而求高度适合用后序遍历

平衡二叉树:掌握递归即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
// 递归：
var isBalanced = function(root){
    const getDepth = function(node){
        if(!node)
            return 0;
        let leftDepth = getDepth(node.left);
        if(leftDepth===-1)
            return -1;
        let rightDepth = getDepth(node.right);
        if(rightDepth===-1)
            return -1;
        if(Math.abs(leftDepth-rightDepth)>1){
            return -1;
        }else{
            return 1+Math.max(leftDepth, rightDepth);
        }
    }
    return !(getDepth(root)===-1);
}

// 迭代：后序遍历(太复杂，仅掌握递归方法即可)
var getHeight = function(curNode){
    let stack = [];
    if(!curNode)
        stack.push(curNode);
    let depth = 0, res = 0;
    while(stack.length){
        let node = stack[stack.length-1];
        if(!node){
            stack.pop();
            stack.push(node);
            stack.push(null);
            depth++;
            node.right && stack.push(node.right);
            node.left && stack.push(node.left);
        }else{
            stack.pop();
            node = stack[stack.length-1];
            stack.pop();
            depth--;
        }
        res = res > depth ? res : depth;
    }
    return res;
}
var isBalanced1 = function(root){
    if(!root)
        return true;
    let queue = [root];
    while(queue.length){
        let node = queue[queue.length-1];
        queue.pop();
        if(Math.abs(getHeight(node.left)-getHeight(node.right))>1)
            return false;
        node.right && queue.push(node.right);
        node.left && queue.push(node.left);
    }
    return true;
}

二叉树的所有路径

描述：

​ 返回所有从根节点到叶子节点的路径

递归与回溯：

递归与回溯

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
var binaryTreePaths = function(root){
    let res = [];
    const getPath = function(node, path){
        if(!node.left && !node.right){
            res.push(path.reduce((pre,cur)=>pre+cur, ''));
            return;
        }
        if(node.left){
            path.push('->'+node.left.val);
            getPath(node.left, path);
            path.pop();
        }
        if(node.right){
            path.push('->'+node.right.val);
            getPath(node.right, path);
            path.pop();
        }
    }
    getPath(root, [''+root.val]);
    return res;
}

// 迭代：前序遍历
var binaryTreePaths1 = function(root){
    let res = [];
    if(!root)
        return res;
    let queue = [root];
    //path=['a->b->c', 'a->b->c->d']
    let path = [''+root.val];
    while(queue.length){
        let node = queue.shift();
        let val = path.shift();
        if(!node.left && !node.right){
            res.push(val);
            continue;
        }else{
            if(node.left){
                queue.push(node.left);
                path.push(val+'->'+node.left.val);
            }
            if(node.right){
                queue.push(node.right);
                path.push(val+'->'+node.right.val);
            }
        }
    }
    return res;
}

左叶子之和（先序遍历）

描述：

​ 计算给定二叉树的所有左叶子之和

思路：

​ 判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。如果该节点的左节点不为空，该节点的左节点的左节点为空，该节点的左节点的右节点为空，则找到了一个左叶子。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
var sumOfLeftLeaves = function(root){
    if(!root)
        return 0;
    let midValue = 0;
    if(root.left&&root.left.left===null&&root.left.right===null)
        midValue = root.left.val;
    let leftValue = sumOfLeftLeaves(root.left);
    let rightValue = sumOfLeftLeaves(root.right);
    return leftValue+rightValue+midValue;
}


var sumOfLeftLeaves1 = function(root){
    if(!root)
        return 0;
    let queue = [root];
    let sum = 0;
    while(queue.length){
        let node = queue.shift();
        if(node.left&&node.left.left===null&&node.left.right===null)
            sum += node.left.val;
        node.left && queue.push(node.left);
        node.right && queue.push(node.right);
    }
    return sum;
}

找树左下角的值

描述：

​ 给定一个二叉树，在树的最后一行找到最左边的值

思路：

​ 递归：深度最大的叶子节点一定是最后一行

​ 迭代：层次遍历

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//找到最左边，使用前序遍历
//首先考虑递归遍历 前序遍历 找到最大深度的叶子节点即可
var findBottomLeftValue = function(root){
    let maxPath = 0, resNode = null;
    const dfsTree = function(node, curPath){
        if(!node.left&&!node.right){
            if(curPath>maxPath){
                maxPath = curPath;
                resNode = node.val;
            }
        }
        node.left && dfsTree(node.left, curPath+1);
        node.right && dfsTree(node.right, curPath+1);
    }
    dfsTree(root, 1);
    return resNode;
}

var findBottomLeftValue1 = function(root){
    if(!root)
        return null;
    let queue = [root];
    let resNode;
    while(queue.length){
        let length = queue.length;
        for(let i=0;i<length;i++){
            let node = queue.shift();
            if(i==0)
                resNode = node.val;
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return resNode;
}

路径总和(会递归)

描述：

1
2
   给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
var hasPathSum = function(root, targetSum){
    if(!root)
        return false;
    const traversal = function(node, cnt){
        if(cnt===0&&!node.left&&!node.right)
            return true;
        if(!node.left&&!node.right)
            return false;
        if(node.left&&traversal(node.left, cnt-node.left.val))
            return true;
        if(node.right&&traversal(node.right, cnt-node.right.val))
            return true;
        return false;
    }
    return traversal(root, targetSum-root.val);
}

var hasPathSum1 = function(root, targetSum){
    if(!root)
        return false;
    let queue = [root];
    let path = [root.val];
    while(queue.length){
        let node = queue.shift();
        let val = path.shift();
        if(!node.left&&!node.right&&val===targetSum)
            return true;
        if(node.left){
            queue.push(node.left);
            path.push(val+node.left.val);
        }
        if(node.right){
            queue.push(node.right);
            path.push(val+node.right.val);
        }
    }
    return false;
}

路径总和ii（会递归）

描述：

1
2
3
给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

说明: 叶子节点是指没有子节点的节点。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
var pathSum = function(root, targetSum){
    if(!root)
        return [];
    let res = [];
    const traversal = function(node, cnt, path){
        if(cnt===0&&!node.left&&!node.right){
            res.push([...path]);
            return;
        }
        if(!node.left&&!node.right)
            return;
        if(node.left){
            path.push(node.left.val);
            traversal(node.left, cnt-node.left.val, path);
            path.pop();
        }
        if(node.right){
            path.push(node.right.val);
            traversal(node.right, cnt-node.right.val, path);
            path.pop();
        }
        return;
    }
    if(!root)
        return res;
    traversal(root, targetSum-root.val, [root.val]);
    return res;
}

var pathSum1 = function(root, targetSum){
    if(!root)
        return [];
    let res = [];
    let queue = [root];
    let paths = [[root.val]];
    let count = [root.val];
    while(queue.length){
        let node = queue.shift();
        let path = paths.shift();
        let cnt = count.shift();
        if(cnt===targetSum&&!node.left&&!node.right){
            res.push(path);
            continue;
        }
        if(node.left){
            queue.push(node.left);
            paths.push([...path, node.left.val]);
            count.push(cnt+node.left.val);
        }
        if(node.right){
            queue.push(node.right);
            paths.push([...path, node.right.val]);
            count.push(cnt+node.right.val);
        }
    }
    return res;
}

从中序与后序遍历序列构造二叉树

1
2
3
4
5
6
7
8
9
10
var buildTree = function(inorder, postorder){
    if(!inorder.length)
        return null;
    const rootVal = postorder.pop();
    let rootIndex = inorder.indexOf(rootVal);
    const root = new TreeNode(rootVal);
    root.left = buildTree(inorder.slice(0, rootIndex), postorder.slice(0, rootIndex));
    root.right = buildTree(inorder.slice(rootIndex+1), postorder.slice(rootIndex));
    return root;
}

从前序与中序遍历序列构造二叉树

1
2
3
4
5
6
7
8
9
10
var buildTree1 = function(preorder, inorder){
    if(!preorder.length)
        return null;
    const rootVal = preorder.shift();
    const index = inorder.indexOf(rootVal);
    const root = new TreeNode(rootVal);
    root.left = buildTree1(preorder.slice(0, index), inorder.slice(0, index));
    root.right = buildTree1(preorder.slice(index), inorder.slice(index+1));
    return root;
}

最大二叉树

描述：

1
2
3
4
5
6
7
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下：

- 二叉树的根是数组中的最大元素。
- 左子树是通过数组中最大值左边部分构造出的最大二叉树。
- 右子树是通过数组中最大值右边部分构造出的最大二叉树。

通过给定的数组构建最大二叉树，并且输出这个树的根节点。

思路：

​ 构造树一般采用的是前序遍历，因为先构造中间节点，然后递归构造左子树和右子树。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
function TreeNode(val, left, right) {
    this.val = (val===undefined ? 0 : val)
    this.left = (left===undefined ? null : left)
    this.right = (right===undefined ? null : right)
}

// 递归
var constructMaximumBinaryTree = function(nums){
    const BuildTree = function(arr, left, right){
        if(left > right)
            return null;
        let maxValue = -1;
        let maxIndex = -1;
        for(let i=left;i<=right;i++){
            if(arr[i]>maxValue){
                maxValue = arr[i];
                maxIndex = i;
            }
        }
        let root = new TreeNode(maxValue);
        root.left = BuildTree(arr, left, maxIndex-1);
        root.right = BuildTree(arr, maxIndex+1, right);
        return root;
    }
    let root = BuildTree(nums, 0, nums.length-1);
    return root;
}

// 迭代
function getMax(arr, left, right){
    let maxValue = -1;
    let maxIndex = -1;
    for(let i=left;i<=right;i++){
        if(arr[i]>maxValue){
            maxValue = arr[i];
            maxIndex = i;
        }
    }
    return {maxIndex, maxValue};
}
var constructMaximumBinaryTree = function(nums) {
    if(nums.length===0)
        return null;
    let root = new TreeNode(0);
    let queue = [root];
    let leftqueue = [0];
    let rightqueue = [nums.length-1];
    while(queue.length){
        let node = queue.shift();
        let left = leftqueue.shift();
        let right = rightqueue.shift();
        let {maxIndex, maxValue} = getMax(nums, left, right);
        node.val += maxValue;
        if(left<=maxIndex-1){
            node.left = new TreeNode(0)
            queue.push(node.left);
            leftqueue.push(left);
            rightqueue.push(maxIndex-1);
        }
        if(maxIndex+1<=right){
            node.right = new TreeNode(0)
            queue.push(node.right);
            leftqueue.push(maxIndex+1);
            rightqueue.push(right);
        }
    }
    return root;
};

合并二叉树

描述：

1
2
给定两个二叉树，两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例：

示例1

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// 递归：前序
var mergeTrees = function(root1, root2){
    if(!root1)
        return root2;
    if(!root2)
        return root1;
    root1.val+=root2.val;
    root1.left = mergeTrees(root1.left, root2.left);
    root1.right = mergeTrees(root1.right, root2.right);
    return root1;
}

// 迭代
var mergeTrees1 = function(root1, root2){
    if(!root1)
        return root2;
    if(!root2)
        return root1;
    let queue = [root1, root2];
    while(queue.length){
        let node1 = queue.shift();
        let node2 = queue.shift();
        node1.val += node2.val;
        if(node1.left&&node2.left){
            queue.push(node1.left);
            queue.push(node2.left);
        }
        if(node1.right&&node2.right){
            queue.push(node1.right);
            queue.push(node2.right);
        }
        //不用进队列，因为node1没有左子树，剩下的节点直接从node2继承就可以了
        if(!node1.left&&node2.left)
            node1.left = node2.left;
        if(!node1.right&&node2.right)
            node1.right = node2.right;
    }
    return root1;
}

二叉搜索树中的搜索

描述：

1
给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 递归
var searchBST = function(root, val){
    if(!root || root.val === val)
        return root;
    if(root.val > val)
        return searchBST(root.left, val);
    if(root.val < val)
        return searchBST(root.right, val);
}

// 迭代
var searchBST = function(root, val){
    while(root){
        if(root.val === val)
            return root;
        else if(root.val < val)
            root = root.right;
        else
            root = root.left;
    }
    return null;
}

验证二叉搜索树

描述：

1
2
3
4
5
6
给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。

思路：

​ 中序遍历下，输出的二叉搜索树节点的数值是有序序列。有了这个特性，验证二叉搜索树，就相当于变成了判断一个序列是不是递增的了。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 递归
const helper = function(root, lower, higher){
    if(!root)
        return true;
    if(root.val <= lower || root.val >= higher)
        return false;
    return helper(root.left, lower, root.val) && helper(root.right, root.val, higher);
}
var isValidBST = function(root){
    return helper(root, -Infinity, Infinity);
}

// 迭代：二叉搜索树中序遍历是递增数组
var isValidBST = function(root){
    let arr = [];
    const getArr = function(root){
        if(!root)
            return;
        getArr(root.left);
        arr.push(root.val);
        getArr(root.right);
    }
    getArr(root);
    for(let i=0;i<arr.length-1;i++)
        if(arr[i]>=arr[i+1])
            return false;
    return true;
}

二叉搜索树的最小绝对差

描述：

1
给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

思路：

​ 遇到在二叉搜索树上求什么最值啊，差值之类的，就把它想成在一个有序数组上求最值，求差值，这样就简单多了。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 递归: 变成数组
var getMininumDifference = function(root){
    let arr = [];
    const buildArr = function(root){
        if(!root)
            return;
        buildArr(root.left);
        arr.push(root.val);
        buildArr(root.right);
    }
    buildArr(root);
    let minValue = Infinity;
    for(let i =0;i<arr.length-1;i++)
        if(arr[i+1]-arr[i]<minValue)
            minValue = arr[i+1]-arr[i];
    return minValue;
}

// 递归：在递归中寻找最小值
// 最小值一定出现在两个相邻节点之间
var getMininumDifference = function(root){
    let res = Infinity;
    // 记录上一个节点
    let preNode = null;
    const inorder = (node)=>{
        if(!node)
            return null;
        inorder(root.left);
        if(preNode)
            res = Math.min(res, node.val-preNode.val);
        preNode = node;
        inorder(node.right);
    }
    inorder(root);
    return res;
}

二叉搜索树中的众数

描述：

1
2
3
4
5
6
7
给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

假定 BST 有如下定义：

结点左子树中所含结点的值小于等于当前结点的值
结点右子树中所含结点的值大于等于当前结点的值
左子树和右子树都是二叉搜索树

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// 递归：利用二叉搜索树的性质
var findMode = function(root){
    let count = 0, maxCount = 1;
    let pre = root, res = [];
    const traverseTree = function(cur){
        if(!cur)
            return;
       	traverseTree(cur.left);
        if(pre.val === cur.val)
            count++;
       	else
            count = 1;
        if(count === maxCount)
            res.push(cur.val);
        else if(count > maxCount){
            res = [];
            maxCount = count;
            res.push(cur.val);
        }
        traverseTree(cur.right);
    }
    traverseTree(root);
    return res;
}

// 递归：不利用二叉搜索树的性质
var findMode = function(root){
    let map = {};
    const traverseTree = function(node){
        if(!node)
            return;
        traverseTree(node.left);
        map.set(node.val, (map.get(node.val)||0)+1);
        traverseTree(node.right);
    }
    traverseTree(root);
    let maxCount = 0;
    let res = [];
    for(let [key, value] of map){
        if(value===maxCount)
            res.push(key);
        if(value>maxCount){
            res = [];
            maxCount = value;
            res.push(key);
        }
    }
    return res;
}

二叉树的最近公共祖先

描述：

1
对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 需要从底向上检查，故使用后序遍历
// 使用递归函数的返回值来说明是否找到节点p或者q
// 还需要返回最近公共节点
var lowestCommonAncestor = function(root, p, q){
    const travelTree = function(root, p, q){
        if(!root || root === p || root === q)
            return root;
        // 左子树
        let left = travelTree(root.left, p, q);
        // 右子树
        let right = travelTree(root.right, p, q);
        if(left && right)
            return root;
        if(!left)
            return right;
        return left;
    }
    return travelTree(root, p, q);
}

二叉搜索树的最近公共祖先

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 递归：
var lowestCommonAncestor = function(root, p, q){
    if(!root)
        return root;
    if(root.val>p.val&&root.val>q.val)
        return lowestCommonAncestor(root.left, p, q);
    if(root.val<p.val&&root.val<q.val)
        return lowestCommonAncestor(root.right, p, q);
    return root;
}

// 迭代
var lowestCommonAncestor1 = function(root, p, q){
    if(!root)
        return null;
    while(root){
        if(root.val>p.val && root.val>q.val)
            root = root.left;
        else if(root.val < q.val && root.val < p.val)
            root = root.right;
        else
            return root;
    }
}

二叉搜索树中的插入操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
var insertIntoBST = function(root, val){
    const setInOrder = (root, val)=>{
        if(!root){
            let node = new TreeNode(val);
            return node;
        }
        if(root.val > val)
            root.left = insertIntoBST(root.left, val);
        else if(root.val < val)
            root.right = insertIntoBST(root.right, val);
        return root;
    }
    return setInOrder(root, val);
}

var insertIntoBST = function(root, val){
    if(!root){
        return new TreeNode(val);
    }else{
        let parent = null;
        let cur = root;
        while(cur){
            parent = cur;
            if(cur.val > val)
                cur = cur.left;
            else
                cur = cur.right;
        }
        let node = new TreeNode(val);
        if(parent.val > node.val)
            parent.left = node;
        else
            parent.right = node;
    }
    return root;
}

删除二叉搜索树中的节点

描述：

1
给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
// 递归:分情况考虑
function getMinNode(root){
    while(root.left)
        root = root.left;
    return root;
}
var deleteNode = function(root, key){
    if(!root)
        return root;
    if(key > root.val){
        root.right = deleteNode(root.right, key);
        return root;
    }else if(key<root.val){
        root.left = deleteNode(root.left, key);
        return root;
    }else{
        // 场景1: 该节点是叶节点
        if(!root.left&&!root.right)
            return null;
        // 场景2: 有一个孩子节点不存在
        if(root.left && !root.right)
            return root.left;
        else if(root.right && !root.left)
            return root.right;
        // 场景3: 左右节点都存在
        const rightNode = root.right;
        // 获取右节点上的最小值
        const minNode = getMinNode(rightNode);
        root.val = minNode.val;
        root.right = deleteNode(root.right, minNode.val);
        return root;
    }
}

// 迭代：找到上一个节点和当前节点
function deleteOneNode(target){
    // target为叶子节点
    if(!target.left&&!target.right)
        return null;
    // target节点没有右子树
    if(!target.right)
        return target.left;
    // target节点没有左子树
    if(!target.left)
        return target.right;
    let cur = target.right;
    // target节点两个子树都有
    while(cur.left)
        cur = cur.left;
    cur.left = target.left;
    return target.right;
}
var deleteNode = function(root, key){
    if(!root)
        return root;
    let cur = root;
    let pre = null;
    while(cur){
        if(cur.val === key)
            break;
        pre = cur;
        cur.val > key ? cur = cur.left:cur = cur.right;
    }
    if(!pre)
        return deleteOneNode(cur);
    if(pre.left && pre.left.val === key)
        pre.left = deleteOneNode(cur);
    if(pre.right && pre.right.val === key)
        pre.right = deleteOneNode(cur);
    return root;
}

修剪二叉搜索树

描述：

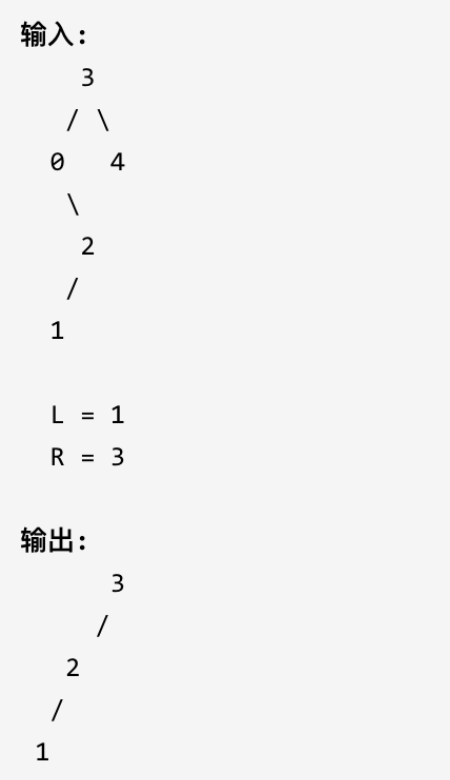
1
给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

示例：

示例1

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
var trimBST = function(root, low, high){
    if(!root)
        return null;
    // 节点值小于最小值
    if(root.val < low)
        return trimBST(root.right, low, high);
    // 节点值大于最大值
    if(root.val > high)
        return trimBST(root.left, low, high)
    // 节点值介于最大值和最小值之间
    root.left = trimBST(root.left, low, high);
    root.right = trimBST(root.right, low, high);
    return root;
}

function trimBST1(root, low, high){
    if(!root)
        return null;
    // 处理头结点，让root移动到[L, R] 范围内，注意是左闭右闭
    while(root && (root.val<low||root.val>high)){
        if(root.val<low)
            root = root.right;
        else
            root = root.left;
    }
    let cur = root;
    // 此时root已经在[L, R] 范围内，处理左孩子元素小于L的情况
    while(cur){
        while(cur.left && cur.left.val<low)
            cur.left = cur.left.right;
        cur = cur.left;
    }
    cur = root;
    // 此时root已经在[L, R] 范围内，处理右孩子大于R的情况
    while(cur){
        while(cur.right && cur.right.val > high)
            cur.right = cur.right.left;
        cur = cur.right;
    }
    return root;
}

将有序数组转换为高度平衡的二叉搜索树

描述：

1
将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
var sortedArrayToBST = function(nums){
    const buildTree = function(arr, left, right){
        if(left > right)
            return null;
        let mid = Math.floor(left+(right-left)/2);
        let root = new TreeNode(arr[mid]);
        root.left = buildTree(arr, left, mid-1);
        root.right = buildTree(arr, mid+1, right);
        return root;
    }
    return buildTree(nums, 0, nums.length-1);
}

var sortedArrayToBST = function(nums){
    if(nums.length===0)
        return null;
    let root = new TreeNode(0);
    let nodeQue = [root];
    let leftQue = [0];
    let rightQue = [nums.length-1];
    while(nodeQue.length){
        let curNode = nodeQue.shift();
        let left = leftQue.shift();
        let right = rightQue.shift();
        let mid = left + Math.floor((right-left)/2);
        curNode.val = nums[mid];
        if(left <= mid-1){
            curNode.left = new TreeNode(0);
            nodeQue.push(curNode?.left);
            leftQue.push(left);
            rightQue.push(mid-1);
        }
        if(right>=mid+1){
            curNode.right = new TreeNode(0);
            nodeQue.push(curNode?.right);
            leftQue.push(mid+1);
            rightQue.push(right);
        }
    }
    return root;
}

把二叉搜索树转换成累加树

描述：

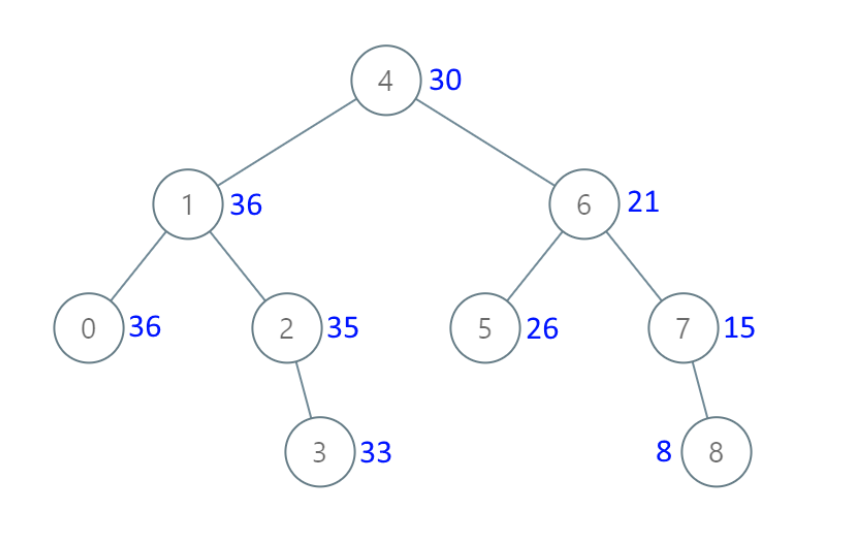
1
2
3
4
给定一个二叉搜索树 root (BST)，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

二叉搜索树满足下列约束条件：
节点的左子树仅包含键 小于 节点键的节点。 节点的右子树仅包含键 大于 节点键的节点。 左右子树也必须是二叉搜索树。

示例：

累加树

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 反中序遍历
var convertBST = function(root){
    let pre = 0;
    const recur = function(root){
        if(!root)
            return;
        recur(root.right);
        root.val += pre;
        pre = root.val;
        recur(root.left);
    }
    recur(root);
    return root;
}

var convertBST = function(root){
    let pre = 0;
    let cur = root;
    let stack = [];
    while(stack.length || cur){
        while(cur){
            stack.push(cur);
            cur = cur.right;
        }
        cur = stack.pop();
        cur.val += pre;
        pre = cur.val;
        cur = cur.left;
    }
    return root;
}

二叉树根节点到叶子节点的路径和

描述：

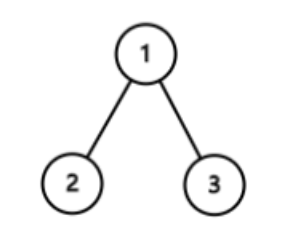
1
2
3
4
5
给定一个二叉树的根节点root，该树的节点值都在数字0−9之间，每一条从根节点到叶子节点的路径都可以用一个数字表示。
1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
2.叶子节点是指没有子节点的节点
3.路径只能从父节点到子节点，不能从子节点到父节点
4.总节点数目为n

示例：

路径和

1
2
3
4
这颗二叉树一共有两条路径，
根节点到叶子节点的路径 1→2 用数字 12 代替
根节点到叶子节点的路径 1→3 用数字 13 代替
所以答案为12+13=25

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 后序遍历
function sumNumbers( root ) {
    if(!root)
      return 0;
    let nodeStack = [];
    let valStack = [];
    let res = 0;
    nodeStack.push(root);
    valStack.push(root.val);
    while(nodeStack.length){
      let node = nodeStack.pop();
      let value = valStack.pop();
      if(!node.left && !node.right)
        res += value;
      else{
        if(node.right){
          nodeStack.push(node.right);
          valStack.push(value*10+node.right.val);
        }
        if(node.left){
          nodeStack.push(node.left);
          valStack.push(value*10+node.left.val);
        }
      }
    }
    return res;
}

二叉树中和为某一值的路径

描述：

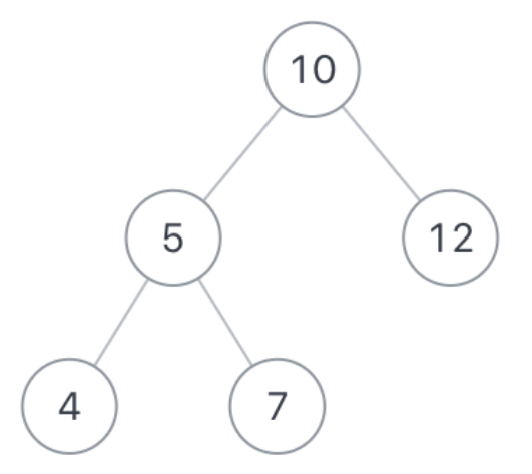
1
2
3
4
5
输入一颗二叉树的根节点root和一个整数expectNumber，找出二叉树中结点值的和为expectNumber的所有路径。
1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
2.叶子节点是指没有子节点的节点
3.路径只能从父节点到子节点，不能从子节点到父节点
4.总节点数目为n

示例：

路径和

1
二叉树root为{10,5,12,4,7},expectNumber为22, 则合法路径有[[10,5,7],[10,12]]

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function find(root, number){
    let res = [];
    let path = [];
    const dfs = (root, number)=>{
        if(!root)
            return null;
        path.push(root.val);
        number -= root.val;
        if(!root.left&&!root.right&&number===0)
            res.push([...path]);
        dfs(root.left, number);
        dfs(root.right, number);
        path.pop();
    }
    dfs(root, number);
    return res;
}

验证二叉完全树

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 判断完全树：使用层次遍历
var isCompleteTree = function(root){
    let queue = [root];
    // 遍历完所有非空节点时变成 true
    let end = false;
    while(queue.length){
        let len = queue.length;
        while(len--){
            let cur = queue.shift();
            if(!cur)
                // 第一次遇到 null 时 end 变成 true，如果之后的所有节点都是 null，则说明是完全二叉树
                end = true;
            else{
                // end 为 true 时遇到非空节点说明不是完全二叉树
                if(end)
                    return false;
                queue.push(cur.left);
                queue.push(cur.right);
            }
        }
    }
    return true;
}

相似题目：

  • 最大二叉树、将有序数组构造成平衡的二叉搜索树
  • 二叉树的所有路径、路径总和、路径总和ii