回溯算法
回溯法一般用于解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
回溯法解决的问题都可以抽象为树形结构。回溯函数也就是递归函数,指的都是一个函数。
回溯函数遍历过程伪代码如下:
1 | for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { |
for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历。这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
分析完过程,回溯算法模板框架如下:
1 | void backtracking(参数) { |
组合(可以看成是有序无重复元素的数组)
描述:
1 | 给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。 |
解法:
1 | let result = []; |
组合总和iii(可以看成是有序无重复元素的数组)
描述:
1 | 找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。 |
解法:
1 | let res = []; |
电话号码的字母组合
描述:
1 | 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 |

解法:
1 | var letterCombinations = function(digits){ |
组合总和(此题中元素可以重复选取)
描述:
1 | 给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。 |
解法:
1 | var combinationSum = function(candidates, target){ |
组合总和ii(可以看成是有序有重复元素的数组)
描述:
1 | 给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 |
示例:
1 | 输入: candidates = [10,1,2,7,6,1,5], target = 8 |
解法:
1 | var sum = function(candidates, target){ |
分割回文串
描述:
1 | 给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。 |
示例:
1 | 输入: "aab" |
解法:
1 | function isPalindrome(str){ |
复原IP地址
描述:
1 | 给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。有效的 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。 |
示例:
1 | 输入:s = "25525511135" |
解法:
1 | var restoreIpAddress = function(s){ |
子集
描述:
1 | 给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。 |
示例:
1 | 输入: nums = [1,2,3] |
解法:
1 | var subsets = function(nums){ |
子集ii
描述:
1 | 给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。 |
示例:
1 | 输入: [1,2,2] |
解法:
1 | var subsets = function(nums){ |
字符串的排列[这题是子集ii、全排列的结合]
链接:
描述:
输入一个长度为 n 字符串,打印出该字符串中字符的所有排列,你可以以任意顺序返回这个字符串数组。例如输入字符串ABC,则输出由字符A,B,C所能排列出来的所有字符串ABC,ACB,BAC,BCA,CBA和CAB。
示例:
1 | 输入:"ab" |
解法:
1 | function Permutation(str) |
递增子序列
描述:
1 | 给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。 |
示例:
1 | 输入: [4, 6, 7, 7] |
解法:
1 | var get = function(nums){ |
全排列
描述:
1 | 给定一个 没有重复 数字的序列,返回其所有可能的全排列 |
示例:
1 | 输入: [1,2,3] |
解法:
1 | var permute = function(nums) { |
全排列ii
描述:
1 | 给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。 |
示例:
1 | 示例 1: |
解法:
1 | var permute = function(nums){ |
重新安排行程
描述:
1 | 给定一个机票的字符串二维数组 [from, to],子数组中的两个成员分别表示飞机出发和降落的机场地点,对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。 |
示例:
1 | 示例 1: |
解法:
1 | var findItinerary = function(tickets){ |
N皇后
描述:
1 | n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。 |
示例:
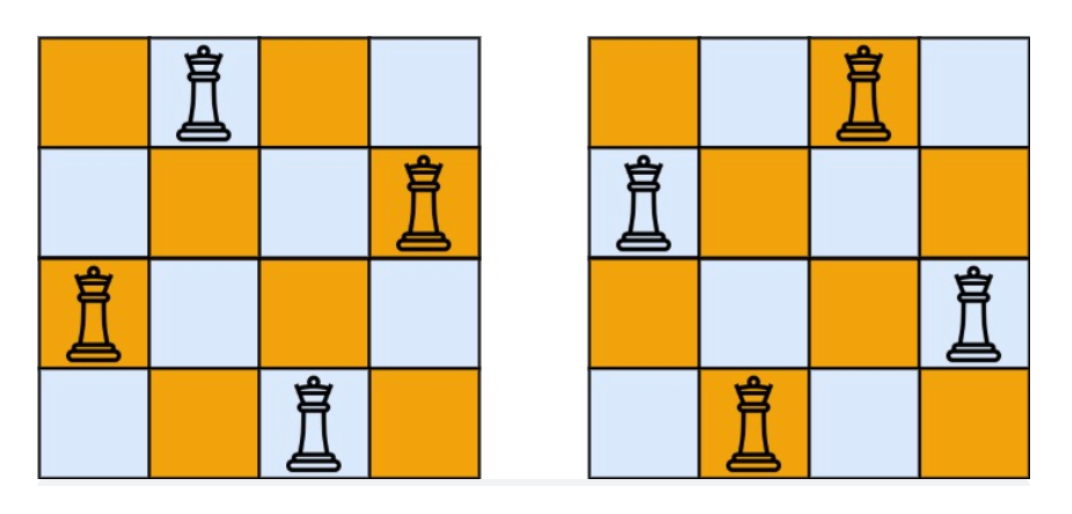
1 | 输入:n = 4 |
思路:
- 不能同行
- 不能同列
- 不能同斜线
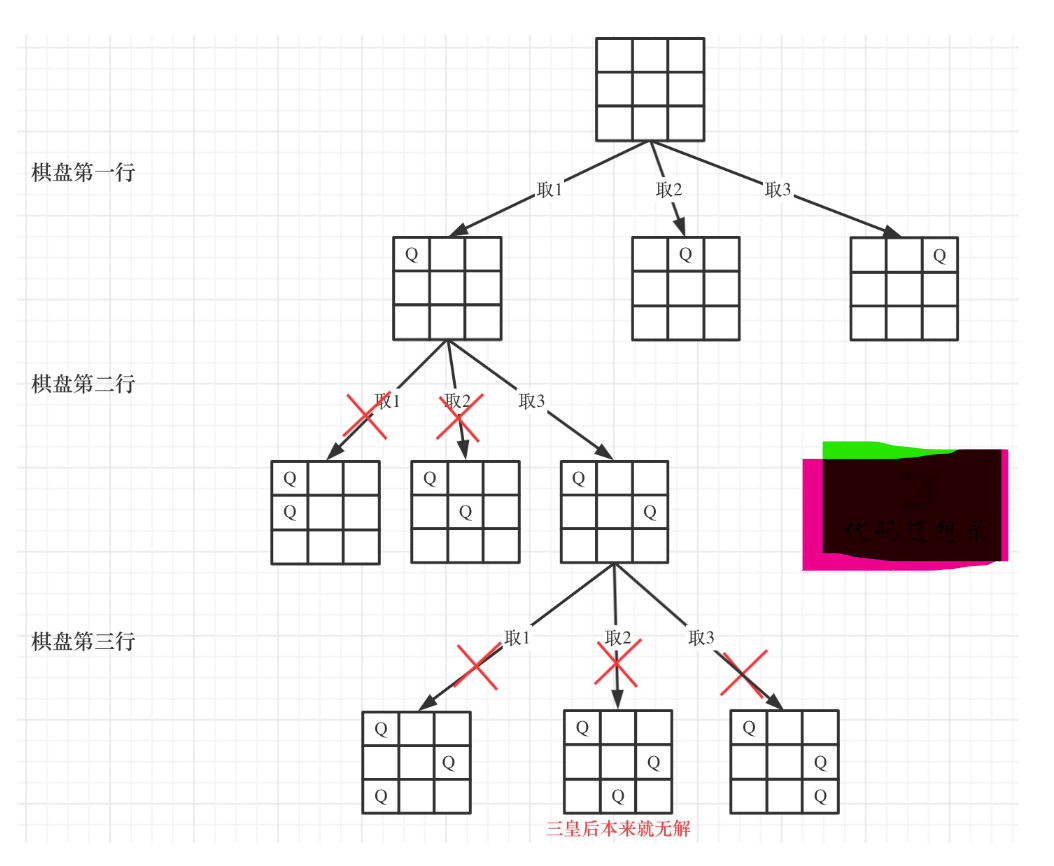
!!!棋盘的宽度就是for循环的长度,递归的深度就是棋盘的高度,这样就可以套进回溯法的模板里了。
解法:
1 | var solveNQueens = function(n){ |
解数独
描述:
1 | 数独的解法需 遵循如下规则: |
示例:
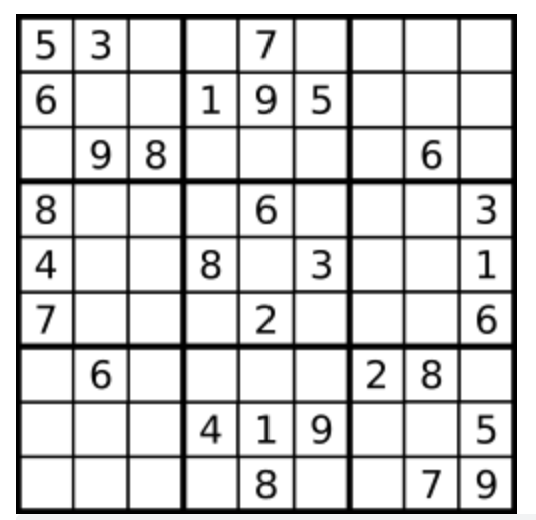
1 | 输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]] |
解法:
1 | var solveSudoku = function(board) { |
相似的题目:
- 子集、子集ii、
- 切割回文串、复原IP地址
- 去重:组合总和ii、递增子序列、全排列、全排列ii
- N皇后、解数独、重新安排行程
- 组合、组合总和iii、电话号码的字母组合、组合总和(可重复)
总结:
- 结果不包含重复数组:回溯中使用startIndex;输入的数组包含重复元素:去重;
- 去重的策略:数组排序(i>startIndex)、记录使用过的元素、记录使用过的元素下标(记录使用的下标需要在回溯算法参数中携带此记录数组[需要pop],记录使用过的元素只需要在回溯算法内部新建数组记录[无需pop])
- 组合总和ii、组合总和这一类当累积和超过目标值时要及时返回,否则会超时
- 递增子序列push完当前path后不能马上返回,因为其他长度的也可以push进去
解数独和重新安排行程需要判断回溯结果是否为true,因为这两个问题都只需要找到一个行程就能返回
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Cheyennee!




