栈与队列

问题：用栈实现队列

问题描述：

使用栈实现队列的下列操作：
push(x) -- 将一个元素放入队列的尾部。
pop() -- 从队列首部移除元素。
peek() -- 返回队列首部的元素。
empty() -- 返回队列是否为空。

示例：

MyQueue queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.peek();  // 返回 1
queue.pop();   // 返回 1
queue.empty(); // 返回 false

解法：

var MyQueue = function(){
    this.stackIn = [];
    this.stackOut = [];
};
MyQueue.prototype.push = function(x){
    this.stackIn.push(x);
}
MyQueue.prototype.pop = function(){
    const size = this.stackOut.length;
    if(size)
        return this.stackOut.pop();
    while(this.stackIn.length)
        this.stackOut.push(this.stackIn.pop());
    return this.stackOut.pop();
}
MyQueue.prototype.peek = function(){
    const x = this.pop();
    this.stackOut.push(x);
    return x;
}
MyQueue.prototype.empty = function(){
    return !this.stackIn.length && !this.stackOut.length;
}

问题：用队列实现栈

问题描述

使用队列实现栈的下列操作：
push(x) -- 元素 x 入栈
pop() -- 移除栈顶元素
top() -- 获取栈顶元素
empty() -- 返回栈是否为空

解法：

//使用两个数组实现
Var MyStack = function(){
    //实际出栈的数组
    this.queue1 = [];
    this.queue2 = [];
}
MyStack.prototype.push = function(x){
    this.queue1.push(x);
}
MyStack.prototype.pop = function(){
    if(!this.queue1.length)
        [this.queue1, this.queue2] = [this.queue2, this.queue1];
    while(this.queue1.length>1)
        this.queue2.push(this.queue1.shift());
    return this.queue1.shift();
}
MyStack.prototype.top = function(){
    const x = this.pop();
    this.queue1.push(x);
    return x;
}
MyStack.prototype.empty = function(){
    return !this.queue1.length&&!this.queue2.length;
}

//使用一个数组实现
var MyStack = function(){
    this.queue = [];
}
MyStack.prototype.push = function(x){
    this.queue.push(x);
}
MyStack.prototype.pop = function(x){
    let size = this.queue.length;
    while(size-- > 1)
        this.queue.push(this.queue.shift());
    return this.queue.shift();
}
MyStack.prototype.top = function(){
    const x = this.pop();
    this.queue.push(x);
    return x;
}
MyStack.prototype.empty = function(){
    return !this.queue.length;
}

有效的括号

问题描述：

输入："()"
输出: true

输入: "(]"
输出: false

解法：

var isValid = function(s){
    let res = [];
    let map = {'(':')', '{':'}', '[':']'};
    for(const t of s){
        if(t in map){
            res.push(t);
            continue;
        }
        if(map[res.pop()]!==x)
            return false;
    }
    return !res.length;
}

括号生成

描述：

给出n对括号，请编写一个函数来生成所有的由n对括号组成的合法组合。例如，给出n=3，解集为：
"((()))", "(()())", "(())()", "()()()", "()(())"

示例：

输入：2
返回值：["(())","()()"]

解法：

function generateParenthesis(n){
    let res = [];
    recursion(0,0,"",res,n);
    return res;
}
function recursion(left, right, temp, res, n){
    if(left===n&&right===n){
        res.push(temp);
        return;
    }
    if(left<n)
        recursion(left+1,right,temp+'(',res,n);
    if(right<n&&left>right)
        recursion(left, right+1, temp+')', res, n);
}

删除字符串中的所有相邻重复项

描述：

输入："abbaca"
输出："ca"
解释：例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

解法：

var removeDuplicates = function(s){
	const stack = [];
    for(const x of s){
        let c = null;
        if(stack.length && x===(c=stack.pop()))
            continue;
        c && stack.push(c);
        stack.push(x);
    }
    return stack.join("");
}

// 自己写的
var removeDuplicates = function(s){
    const stack = [];
    let length = 0;
    for(const x of s){
        length = stack.length;
        if(length&&stack[length-1]===x)
            stack.pop();
        else{
            stack.push(x);
        }
    }
    return stack.join("");
}

逆波兰表达式求值

描述：

示例 1：
输入: ["2", "1", "+", "3", " * "]
输出: 9
解释: 该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：
输入: ["4", "13", "5", "/", "+"]
输出: 6
解释: 该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

解法：

var evalRPN = function(tokens){
    const s = new Map([
        ["+", (a,b)=>a*1+b*1],
        ["-", (a,b)=>b-a],
        ["*", (a,b)=>b*a],
        ["/", (a,b)=>(b/a)|0]
    ]);
    const stack = [];
    for(const i of tokens){
        if(!s.has(i)){
            stack.push(i);
            continue;
        }
        stack.push(s.get(i)(stack.pop(), stack.pop()));
    }
    return stack.pop();
}

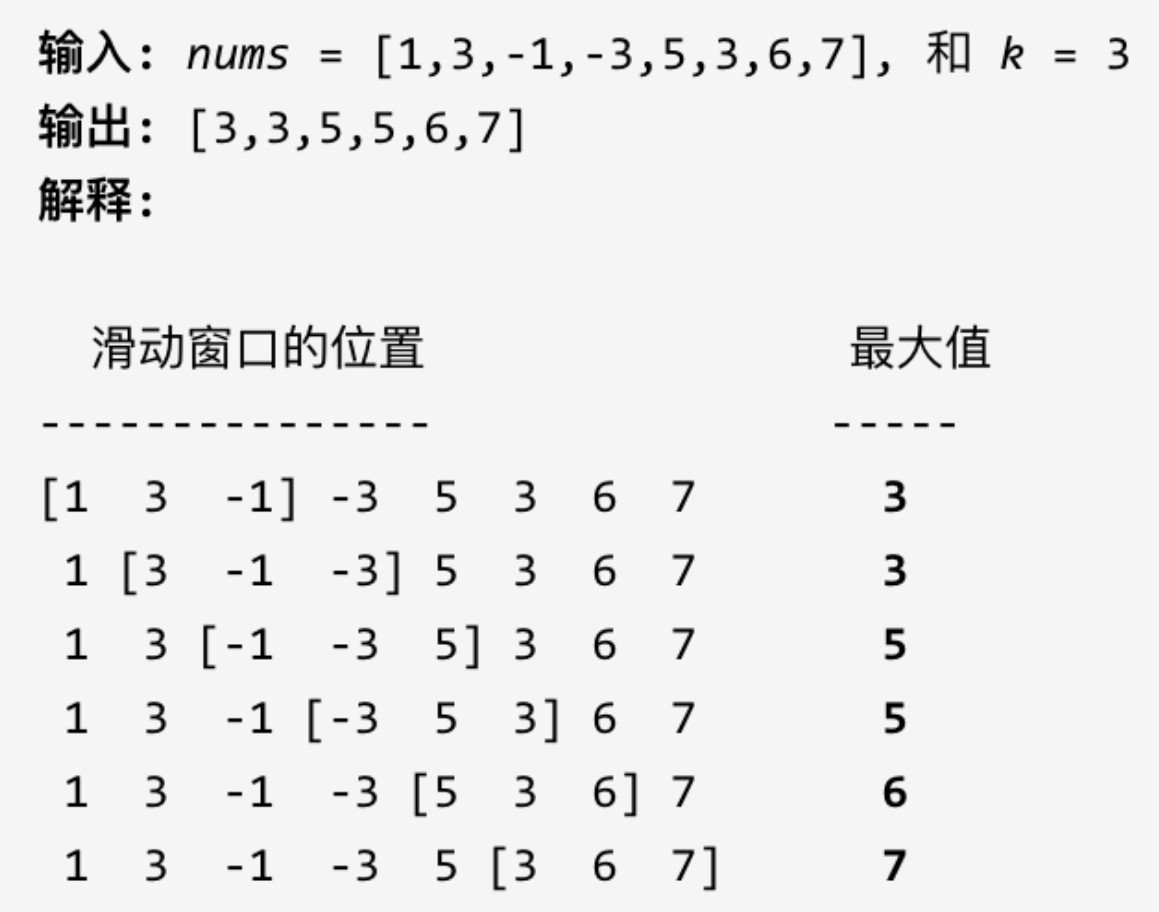
滑动窗口最大值

描述：

思路：

​ 需要一个队列，放进去窗口里的元素，然后随着窗口的移动，队列也一进一出，每次移动之后，队列告诉我们里面的最大值是什么。

​ 队列里的元素一定是要排序的，而且要最大值放在出队口，要不然怎么知道最大值呢。

​ 需要一个单调队列：队列里的元素是单调递减或递增的。

​ 队列前面的元素如果比当前元素小，那么弹出前面的元素。如果队列前面的元素比当前元素大，那么直接加入当前元素即可。如果当前滑动窗口要Pop掉的元素与队列中的最大值相同，则要把队列中的最大值pop掉。

解法：

var maxSlidingWindow = function(nums, k){
    class MonoQueue{
        queue;
        constructor(){
            this.queue = [];
        }
        enqueue(value){
            let back = this.queue[this.queue.length-1];
            //如果队列中有比当前元素小的则直接pop掉
            while(back!==undefined&&back<value){
                this.queue.pop();
                back = this.queue[this.queue.length-1];
            }
            this.queue.push(value);
        }
        dequeue(value){
            let front = this.front();
            //如果当前队列中最大值=需要出队的元素，则将最大值pop掉
            if(front === value)
                this.queue.shift();
        }
        //队头始终是最大值
        front(){
            return this.queue[0];
        }
    }
    
    let helperQueue = new MonoQueue();
    //i表示需要弹出的元素，j表示需要进入的元素
    let i = 0, j=0;
    let resArr = [];
    while(j<k)
        helperQueue.enqueue(nums[j++]);
    resArr.push(helperQueue.front());
    while(j<nums.length){
        helperQueue.enqueue(nums[j]);
        helperQueue.dequeue(nums[i]);
        resArr.push(helperQueue.front());
        i++;
        j++;
    }
    return resArr;
}

前k个高频元素

描述：

示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

思路：

• 统计元素出现的频率：map
• 对频率排序：优先级队列(队头取元素，从队尾添加元素，内部元素是自动依照元素的权值排列)小顶堆
• 找出前k个高频元素

解法：

var topKFrequent = function(nums, k){
    const countMap = {};
    for(let num of nums)
        countMap.set(num, (countMap.get(num)||0)+1);
    //entries是返回[key, value]
    return [...countMap.entries()]
    	.sort((a,b)=>b[1]-a[1])
    	.slice(0, k)
    	.map(i=>i[0])
}

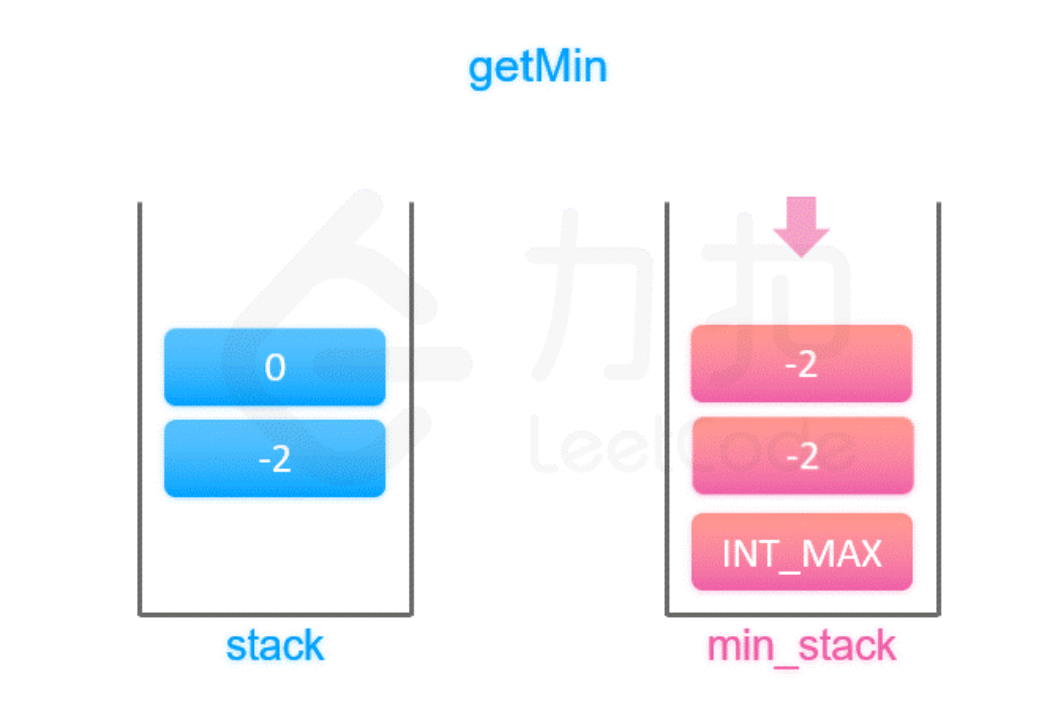
最小栈

描述：

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:
- MinStack() 初始化堆栈对象。
- void push(int val) 将元素val推入堆栈。
- void pop() 删除堆栈顶部的元素。
- int top() 获取堆栈顶部的元素。
- int getMin() 获取堆栈中的最小元素。

示例：

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

思路：

​ 栈顶端是当前最小值。每放进一个元素就去保存当前最小值。

解法：

var MinStack = function() {
    this.stack = [];
    this.minStack = [Infinity];
};

/** 
 * @param {number} val
 * @return {void}
 */
MinStack.prototype.push = function(val) {
    this.stack.push(val);
    this.minStack.push(Math.min(val, this.minStack[this.minStack.length-1]));
};

/**
 * @return {void}
 */
MinStack.prototype.pop = function() {
    this.stack.pop();
    this.minStack.pop();
};

/**
 * @return {number}
 */
MinStack.prototype.top = function() {
    return this.stack[this.stack.length-1];
};

/**
 * @return {number}
 */
MinStack.prototype.getMin = function() {
    return this.minStack[this.minStack.length-1];
};