top

问题：两数之和

问题描述：

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例：

输入：nums = [2, 7, 11, 15], target = 9
输出：[0, 1]
解释：nums[0] + nums[1] = 2 + 7 = 9

解法：

var twoSum = function(nums, target){
    let hash = {};
    for(let i=0;i<nums.length;i++){
        if(hash[target-nums[i]] !== undefined)
            return [i, hash[target-nums[i]]];
        hash[nums[i]] = i;
    }
    return [];
}

问题：三数之和

问题描述：

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。

注意： 答案中不可以包含重复的三元组。

示例：

输入：nums = [-1, 0, 1, 2, -1, -4]
输出：[ [-1, 0, 1], [-1, -1, 2] ]
//与两数相加的例子不同，此处只要返回数字，而两数相加需要返回索引，所以两数相加不适合用双指针

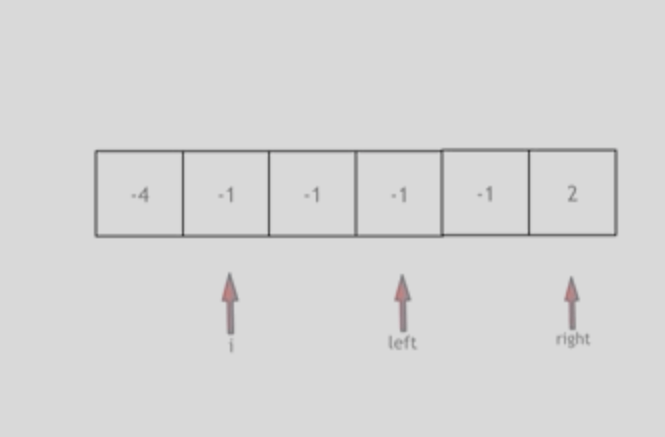
解法图示（双指针）：

细节 - 需要去重，不能有重复的三元组，但是三元组内的元素是可以重复的：

//应该的写法
if (i > 0 && nums[i] == nums[i - 1]) {
    continue;
}
//不应该这么操作：会把三元组中出现重复元素的情况直接pass掉
if (nums[i] == nums[i + 1]) { // 去重操作
    continue;
}

解法：

var threeSum = function(nums){
    const res = [], len = nums.length;
    nums.sort((a, b)=>a-b);
    for(let i=0;i<len;i++){
        let left = i+1, right=len-1,iNum = nums[i];
        if(iNum>0)
            return res;
        //结果去重
        if(iNum===nums[i-1])
            continue;
        while(left<right){
            let lNum = nums[left], rNum = nums[right], threeSum = nums[i]+lNum+rNum;
            if(threeSum<0)
                left++;
            else if(threeSum>0)
                right--;
            else{
                res.push([iNum, lNum, rNum]);
                //去重
                while(left<right&&nums[left]==nums[left+1])
                    ++left;
                while(left<right&&nums[right]==nums[right-1])
                    --right;
            }
            left++;
            right--;
        }
    }
    return res;
}

相加

描述：

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。
请你将两个数相加，并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例：

输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8](链表)
解释：342 + 465 = 807.

解法：

var addTwoNumbers = function(l1, l2){
    let head = null, tail = null;
    let carry = 0;
    while(l1 || l2){
        const n1 = l1?l1.val:0;
        const n2 = l2?l2.val:0;
        const sum = n1+n2+carry;
        if(!head)
            head = tail = new ListNode(sum%10);
        else{
            tail.next = new ListNode(sum%10);
            tail = tail.next;
        }
        carry = Math.floor(sum/10);
        if(l1)
            l1 = l1.next;
        if(l2)
            l2 = l2.next;
    }
    if(carry>0)
        tail.next = new ListNode(carry);
    return head;
}

无重复字符的最长子串

描述：

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例：

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

解法：

var lengthOfLongestSubstring = function (s) {
    // 不要使用{}，会有测试样例不通过的
    let map = new Map();
    let left = 0;
    let maxLen = 0;
    for (let i = 0; i < s.length; i++) {
        let char = s[i];
        if (map.has(char)) {
            left = Math.max(map.get(char) + 1, left);
        }
        map.set(char, i);
        maxLen = Math.max(maxLen, i - left + 1);
    }
    return maxLen;
}

寻找两个正序数组的中位数

描述：

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。

示例：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

解法：

// 时间复杂度：o(log(m+n))
/*
    这个题目可以归结到寻找第k小(大)元素问题，
    思路可以总结如下：取两个数组中的第k/2个元素进行比较，如果数组1的元素小于数组2的元素，
    则说明数组1中的前k/2个元素不可能成为第k个元素的候选，所以将数组1中的前k/2个元素去掉，
    组成新数组和数组2求第k-k/2小的元素，因为我们把前k/2个元素去掉了，所以相应的k值也应该减小。
    另外就是注意处理一些边界条件问题，比如某一个数组可能为空或者k为1的情况。
*/

var findMedianSortedArrays = function (nums1, nums2) {
    let m = nums1.length;
    let n = nums2.length;
    // 小trick
    /*
        分别找第 (m+n+1) / 2 个，和 (m+n+2) / 2 个，然后求其平均值即可，这对奇偶数均适用。
        加入 m+n 为奇数的话，那么其实 (m+n+1) / 2 和 (m+n+2) / 2 的值相等，
        相当于两个相同的数字相加再除以2，还是其本身。
    */
    let left = Math.floor((m + n + 1) / 2);
    let right = Math.floor((m + n + 2) / 2);
    return (findKth(nums1, 0, nums2, 0, left) + findKth(nums1, 0, nums2, 0, right)) / 2;
};
var findKth = function (nums1, start1, nums2, start2, k) {
    if (start1 >= nums1.length) {
        return nums2[start2 + k - 1];
    }
    if (start2 >= nums2.length) {
        return nums1[start1 + k - 1];
    }
    if (k === 1) {
        return Math.min(nums1[start1], nums2[start2]);
    }
    let midVal1 = (start1 + Math.floor(k / 2) - 1 < nums1.length) ? nums1[start1 + Math.floor(k / 2) - 1] : Infinity;
    let midVal2 = (start2 + Math.floor(k / 2) - 1 < nums2.length) ? nums2[start2 + Math.floor(k / 2) - 1] : Infinity;
    if (midVal1 < midVal2) {
        return findKth(nums1, start1 + Math.floor(k / 2), nums2, start2, k - Math.floor(k / 2));
    } else {
        return findKth(nums1, start1, nums2, start2 + Math.floor(k / 2), k - Math.floor(k / 2));
    }
}

最长回文子串

描述：

给你一个字符串 s，找到 s 中最长的回文子串。如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

解法：

var longestPalindrome = function (s) {
    let n = s.length;
    if (n < 2)
        return s;
    let dp = new Array(n).fill([]).map(() => new Array(n));
    for (let i = 0; i < n; i++)
        dp[i][i] = true;
    let maxlen = 1;
    let begin = 0;
    for (let len = 2; len < n + 1; len++) {
        for (let i = 0; i < n; i++) {
            let j = len + i - 1;
            if (j >= n)
                break;
            if (s[i] !== s[j])
                dp[i][j] = false;
            else {
                if (j - i < 3)
                    dp[i][j] = true;
                else
                    dp[i][j] = dp[i + 1][j - 1];
            }
            if (dp[i][j] && (j - i + 1 > maxlen)) {
                maxlen = j - i + 1;
                begin = i;
            }
        }
    }
    return s.substring(begin, begin + maxlen);
};

盛最多水的容器

描述：

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。

示例：

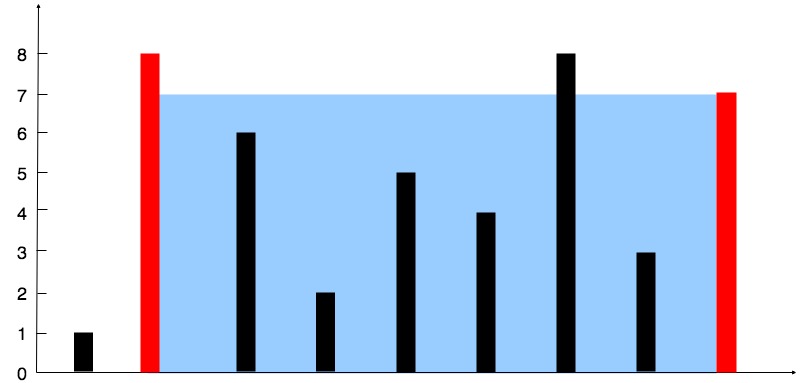
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

解法：

/*
 一开始两个指针一个指向开头一个指向结尾，此时容器的底是最大的，接下来随着指针向内移动，会造成容器的底变小，
 在这种情况下想要让容器盛水变多，就只有在容器的高上下功夫。 那我们该如何决策哪个指针移动呢？
 我们能够发现不管是左指针向右移动一位，还是右指针向左移动一位，容器的底都是一样的，都比原来减少了 1。
 这种情况下我们想要让指针移动后的容器面积增大，就要使移动后的容器的高尽量大，
 所以我们选择指针所指的高较小的那个指针进行移动，这样我们就保留了容器较高的那条边，放弃了较小的那条边，
 以获得有更高的边的机会。
 应该是贪心算法的思路。
*/

var maxArea = function (height) {
    let size = height.length;
    let left = 0, right = size - 1;
    let ans = 0;
    while (left < right) {
        ans = Math.max(ans, (right - left) * Math.min(height[left], height[right]));
        if (height[left] > height[right]) {
            right--;
        } else {
            left++;
        }
    }
    return ans;
}

电话号码的字母组合

描述：

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

解法：

var letterCombinations = function (digits) {
    const k = digits.length;
    const map = ["", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"];
    if (k === 0) {
        return [];
    }
    if (k === 1) {
        return map[digits].split('');
    }
    let res = [], path = [];
    function backtracking(digits, k, startIndex) {
        if (path.length === k) {
            res.push(path.join(""));
            return;
        }
        for (const v of map[digits[startIndex]]) {
            path.push(v);
            backtracking(digits, k, startIndex + 1);
            path.pop(v);
        }
    }
    backtracking(digits, k, 0);
    return res;
}

删除链表的倒数第 N 个结点

描述：

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例：

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

解法：

var removeNthFromEnd = function (head, n) {
    let slow = head, fast = head;
    while (n-- && fast !== null) {
        fast = fast.next;
    }
    // 说明n太大了，则删除头节点
    if (fast === null) {
        return head.next;
    }
    while (fast.next !== null) {
        fast = fast.next;
        slow = slow.next;
    }
    slow.next = slow.next.next;
    return head;
}

有效的括号

描述：

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。
有效字符串需满足：
-左括号必须用相同类型的右括号闭合。
-左括号必须以正确的顺序闭合。
-每个右括号都有一个对应的相同类型的左括号。

示例：

输入：s = "()"
输出：true

解法：

var isValid = function (s) {
    let map = { '(': ")", "[": "]", "{": "}" };
    if (s.length % 2) {
        return false;
    }
    let stack = [];
    for (let i = 0; i < s.length; i++) {
        if (Object.keys(map).includes(s[i])) {
            stack.push(s[i]);
        } else {
            if (stack.length === 0) {
                return false;
            }
            const top = stack.pop();
            if (map[top] !== s[i]) {
                return false;
            }
        }
    }
    return stack.length === 0;
};

合并两个有序链表

描述：

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

解法：

var mergeTwoLists = function(l1, l2){
    const prehead = new ListNode(-1);
    let prev = prehead;
    while(l1 && l2){
        if(l1.val < l2.val){
            prev.next = l1;
            l1 = l1.next;
        }else{
            prev.next = l2;
            l2 = l2.next;
        }
        prev = prev.next;
    }
    prev.next = l1 ? l1 : l2;
    return prehead.next;
}

合并K个有序链表

解法：

// 两两合并
var mergeKLists = function (lists) {
    if (lists.length === 0) {
        return null;
    }
    let ans = lists[0];
    for (let i = 1; i < lists.length; i++) {
        ans = mergeTwoLists(ans, lists[i]);
    }
    return ans;
};

var mergeTwoLists = function (l1, l2) {
    const prehead = new ListNode(-1);
    let prev = prehead;
    while (l1 && l2) {
        if (l1.val < l2.val) {
            prev.next = l1;
            l1 = l1.next;
        } else {
            prev.next = l2;
            l2 = l2.next;
        }
        prev = prev.next;
    }
    prev.next = l1 ? l1 : l2;
    return prehead.next;
}

// 归并
var mergeKLists = function (lists) {
    return merge(lists, 0, lists.length - 1);
}
var merge = function (lists, l, r) {
    if (l === r) {
        return lists[l];
    }
    if (l > r) {
        return null;
    }
    const mid = Math.floor((l + r) / 2);
    return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
}

下一个排列

描述：

整数数组的一个 排列  就是将其所有成员以序列或线性顺序排列。
例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。
例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ，找出 nums 的下一个排列。
必须 原地 修改，只允许使用额外常数空间。

示例：

输入：nums = [1,2,3]
输出：[1,3,2]

解法：

/*
我们希望下一个数 比当前数大，这样才满足 “下一个排列” 的定义。因此只需要 将后面的「大数」与前面的「小数」交换，就能得到一个更大的数。比如 123456，将 5 和 6 交换就能得到一个更大的数 123465。
我们还希望下一个数 增加的幅度尽可能的小，这样才满足“下一个排列与当前排列紧邻“的要求。为了满足这个要求，我们需要：
在 尽可能靠右的低位 进行交换，需要 从后向前 查找
将一个 尽可能小的「大数」 与前面的「小数」交换。比如 123465，下一个排列应该把 5 和 4 交换而不是把 6 和 4 交换
将「大数」换到前面后，需要将「大数」后面的所有数 重置为升序，升序排列就是最小的排列。以 123465 为例：首先按照上一步，交换 5 和 4，得到 123564；然后需要将 5 之后的数重置为升序，得到 123546。显然 123546 比 123564 更小，123546 就是 123465 的下一个排列
*/

var nextPermutation = function (nums) {
    if(nums.length <= 1){
        return;
    }
    let i = nums.length - 2, j = nums.length - 1, k = nums.length - 1;
    // 先从后往前寻找一个递增序列，j之后的数字肯定是递减的
    while(i>=0 && nums[i] >= nums[j]){
        i--;
        j--;
    }
    if(i>=0){
        // 将寻找的nums[i]与后面递减数组中的最小的大于nums[i]的数进行交换
        // 这样使得改动尽可能小
        while(nums[i] >= nums[k]){
            k--;
        }
        [nums[i], nums[k]] = [nums[k], nums[i]];
    }
    // 使j开始的数组变成递增，使得变大的幅度最小
    i = j;
    j = nums.length - 1;
    while(i < j){
        [nums[i], nums[j]] = [nums[j], nums[i]];
        i++;
        j--;
    }
}

最长有效括号

描述：

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例：

输入：s = "(()"
输出：2
解释：最长有效括号子串是 "()"

解法：

var longestValidParentheses = function (s) {
    let n = s.length;
    let dp = new Array(n).fill(0);
    let maxLen = 0;
    for (let i = 1; i < n; i++) {
        if (s[i] === ')') {
            if (s[i - 1] === '(') {
                dp[i] = 2;
                if (i - 2 >= 0) {
                    dp[i] = dp[i - 2] + 2;
                }
            } else if (dp[i - 1] > 0) {
                let lastIndex = i - dp[i - 1] - 1;
                if (lastIndex >= 0 && s[lastIndex] === '(') {
                    dp[i] = dp[i - 1] + 2;
                    if (lastIndex - 1 >= 0) {
                        dp[i] = dp[i] + dp[lastIndex - 1];
                    }
                }
            }
        }
        maxLen = Math.max(maxLen, dp[i]);
    }
    return maxLen;
}

搜索旋转排序数组

描述：

整数数组 nums 按升序排列，数组中的值互不相同 。
在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

解法：

var search = function (nums, target) {
    let n = nums.length;
    if (!n) {
        return -1;
    }
    if (n === 1) {
        return nums[0] === target ? 0 : -1;
    }
    let left = 0, right = nums.length - 1;
    while (left <= right) {
        let mid = Math.floor((left + right) / 2);
        if (nums[mid] === target) {
            return mid;
        }
        if (nums[0] <= nums[mid]) {
            if (nums[0] <= target && target < nums[mid]) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        } else {
            if (nums[mid] < target && target <= nums[n - 1]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
    }
    return -1;
}

在排序数组中查找元素的第一个和最后一个位置

描述：

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target，返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

解法：

// 这道题是二分法左闭右开的变形
var searchRange = function(nums, target){
    let left = search(nums, target);
    let right = search(nums, target+1);
    if(left === nums.length || nums[left] !== target){
        return [-1, -1];
    }
    return [left, right-1];
}

var search = function(nums, target){
    let left = 0, right = nums.length;
    while(left < right){
        let mid = Math.floor((left+right)/2);
        if(nums[mid] >= target){
            right = mid;
        }else{
            left = mid + 1;
        }
    }
    return left;
}

组合总和

描述：

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。 
对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

解法：

// 可重复选取元素
// 无重复元素的有序数组
var combinationSum = function (candidates, target) {
    const res = [];
    const path = [];
    candidates.sort((a, b) => a - b);
    function backtracking(startIndex, sum) {
        if (sum === target) {
            res.push(Array.from(path));
            return;
        }
        for (let i = startIndex; i < candidates.length; i++) {
            const n = candidates[i];
            if (n > target - sum) {
                break;
            }
            path.push(n);
            sum += n;
            backtracking(i, sum);
            path.pop();
            sum -= n;
        }
    }
    backtracking(0, 0);
    return res;
}

// 有重复元素的有序数组
var sum = function(candidates, target){
    const res = [];
    const path = [];
    candidates.sort((a, b)=>a-b);
    function backtracking(startIndex, sum){
        if(sum === target){
            res.push(Array.from(path));
            return;
        }
        if(sum > target){
            return;
        }
        for(let i=startIndex;i<candidates.length;i++){
            if(i>startIndex && candidates[i] === candidates[i-1])
                continue;
            const n = candidates[i];
            if(n > target - sum){
                break;
            }
            sum += n;
            path.push(n);
            backtracking(i+1, sum);
            path.pop();
            sum -= n;
        }
    }
    backtracking(0, 0);
    return res;
}

let res = combinationSum([2, 2, 2, 2], 6);
console.log(res);

接雨水

描述：

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

解法：

// 单调递减栈，2-1-3，才能形成凹槽，按行来计算量
var trap = function (height) {
    let len = height.length;
    if (len < 2) {
        return 0;
    }
    let stack = [0];
    let sum = 0;
    let lastIndex = 1;
    for (let i = 1; i < len; i++) {
        if (height[i] < height[stack[lastIndex]]) {
            stack.push(i);
            lastIndex++;
        } else if (height[i] === height[stack[lastIndex]]) {
            stack[lastIndex] = i;
        } else {
            while (stack.length && height[i] > height[stack[lastIndex]]) {
                let mid = stack[lastIndex];
                lastIndex--;
                stack.pop();
                if (stack.length) {
                    let h = Math.min(height[stack[lastIndex]], height[i]) - height[mid];
                    let w = i - stack[lastIndex] - 1;
                    sum += h * w;
                }
            }
            stack.push(i);
            lastIndex++;
        }
    }
    return sum;
}

全排列

解法：

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

描述：

var permute = function (nums) {
    let res = [];
    let path = [];
    function backtracking(used) {
        if (path.length === nums.length) {
            res.push(Array.from(path));
            return;
        }
        for (let i = 0; i < nums.length; i++) {
            if (used[i]) {
                continue;
            }
            path.push(nums[i]);
            used[i] = true;
            backtracking(used);
            used[i] = false;
            path.pop();
        }
    }
    backtracking([]);
    return res;
}

旋转图像

描述：

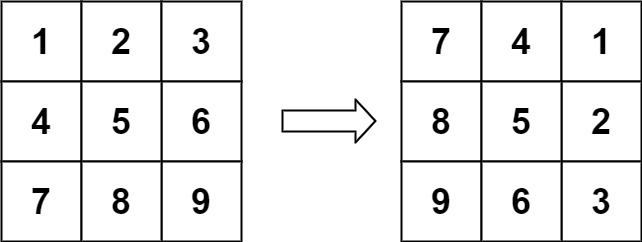
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

字母异位词分组

描述：

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

示例：

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

解法：

// 排序
var groupAnagrams = function (strs) {
    const map = new Map();
    for (let str of strs) {
        let arr = Array.from(str);
        arr.sort();
        // 使用toString方法将数组转成key
        let key = arr.toString();
        let list = map.get(key) ? map.get(key) : [];
        list.push(str);
        map.set(key, list);
    }
    return Array.from(map.values());
}

// hash + 计数
var groupAnagrams = function (strs) {
    const map = {};
    for (let s of strs) {
        const count = new Array(26).fill(0);
        for (let c of s) {
            count[c.charCodeAt() - 'a'.charCodeAt()]++;
        }
        map[count] ? map[count].push(s) : map[count] = [s];
    }
    return Object.values(map);
}

最大子数组和

描述：

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
子数组 是数组中的一个连续部分。

示例：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

解法：

// 使用动态规划便于理解
// dp[i]表示到第i个元素的最大连续子序和
// 所以最后还需要比较这length个元素的最大自序和
var maxSubArray = function (nums) {
    let dp = new Array(nums.length);
    dp[0] = nums[0];
    let res = nums[0];
    for (let i = 1; i < nums.length; i++) {
        if (dp[i - 1] < 0) {
            dp[i] = nums[i];
        } else {
            dp[i] = nums[i] + dp[i - 1];
        }
        res = Math.max(res, dp[i]);
    }
    return res;
}